Bayesian Bivariate Latent CLass Meta-analysis Model
Saliva_COVID DATASET
The Saliva_COVID database includes 6013 participants spread across 17 studies as follow. The Saliva_COVID data is from Butler-Laporte et al(2021)
BAYESIAN BIVARIATE LATENT CLASS META-ANALYSIS MODEL ASSUMING CONDITIONNAL INDEPENDENCE
# Bayesian bivariate model
if(Cond.Dep == TRUE){
modelString =
"model {
#=================================================================
############ LIKELIHOOD ############
#=================================================================
for(i in 1:N) {
# The 4 cells in the two-by-two table of the new test vs. the imperfect reference standard in each study in the meta-analysis
cell[i,1:4] ~ dmulti(prob[i,1:4],n[i])
# Multinomial probabilities of the 4 cells of the two-by-two table expressed in terms of the disease prevalence (prev), the sensitivity (se1, se2) and specificity (sp1, sp2) of the two tests and the covariance between them among disease positive (covs12) and disease negative (covc12) groups
se[i] <- p[1,i]
sp[i] <- 1-p[2,i]
prob[i,1] <- prev[i]*( p[1,i] * se2[i] + covp[i] ) + (1-prev[i])*( p[2,i] *(1-sp2[i]) + covn[i] )
prob[i,2] <- prev[i]*( p[1,i] * (1-se2[i]) - covp[i] ) + (1-prev[i])*( p[2,i] *sp2[i] - covn[i] )
prob[i,3] <- prev[i]*( (1-p[1,i]) * se2[i] - covp[i] ) + (1-prev[i])*( (1-p[2,i]) *(1-sp2[i]) - covn[i] )
prob[i,4] <- prev[i]*( (1-p[1,i]) * (1-se2[i]) + covp[i] ) + (1-prev[i])*( (1-p[2,i]) *sp2[i] + covn[i] )
#=================================================================
############ CONDITIONAL DEPENDENCE ############
#=================================================================
#=======================================
# upper limits of covariance parameters
#=======================================
us[i]<-min(se[i],se2[i])-(se[i]*se2[i]);
uc[i]<-min(sp[i],sp2[i])-(sp[i]*sp2[i]);
ls[i]<- -(1-se[i])*(1-se2[i])
lc[i]<- -(1-sp[i])*(1-sp2[i])
#==============================================================
# prior distribution of transformed covariances on (0,1) range
#==============================================================
covp[i]~dunif(ls[i],us[i]);
covn[i]~dunif(lc[i],uc[i]);
#=================================================================
############ HIERARCHICAL PRIORS ############
#=================================================================
#=======================================
# Hierarchichal prior for xpert
#=======================================
logit(p[1, i]) <- l[i,1]
logit(p[2, i]) <- -l[i,2]
l[i,1:2] ~ dmnorm(mu[], T[,])
#=======================================
# Prior distribution on prevalence
#=======================================
prev[i] ~ dbeta(1,1)
}
# ==================================
# Hierarchical prior for CULTURE
# ==================================
for(j in 1:N) {
logit(se2[j]) <- l2[j,1]
logit(sp2[j]) <- l2[j,2]
l2[j,1:2] ~ dmnorm(mu2[1:2], T2[1:2,1:2])
}
#=================================================================
############ HYPER PRIOR DISTRIBUTIONS ################
#=================================================================
### INDEX TEST
#=================================================================
### prior for the logit transformed sensitivity (mu[1]) and specificity (mu[2])
mu[1] ~ dnorm(0,0.25)
mu[2] ~ dnorm(0,0.25)
T[1:2,1:2]<-inverse(TAU[1:2,1:2])
#### BETWEEN-STUDY VARIANCE-COVARIANCE MATRIX
TAU[1,1] <- tau[1]*tau[1]
TAU[2,2] <- tau[2]*tau[2]
TAU[1,2] <- rho*tau[1]*tau[2]
TAU[2,1] <- rho*tau[1]*tau[2]
#### prec = between-study precision in the logit(sensitivity) and logit(specificity)
prec[1] ~ dgamma(2,0.5)
prec[2] ~ dgamma(2,0.5)
rho ~ dunif(-1,1)
#=================================================================
### REFERENCE TEST
#=================================================================
### prior for the logit transformed sensitivity (mu2[1]) and specificity (mu2[2])
mu2[1] ~ dnorm(0,0.25)
mu2[2] ~ dnorm(0,0.25)
T2[1:2,1:2]<-inverse(TAU2[1:2,1:2])
#### BETWEEN-STUDY VARIANCE-COVARIANCE MATRIX
TAU2[1,1] <- tau2[1]*tau2[1]
TAU2[2,2] <- tau2[2]*tau2[2]
TAU2[1,2] <- rho2*tau2[1]*tau2[2]
TAU2[2,1] <- rho2*tau2[1]*tau2[2]
#### prec = between-study precision in the logit(sensitivity) and logit(specificity)
prec2[1] ~ dgamma(2,0.5)
prec2[2] ~ dgamma(2,0.5)
rho2 ~ dunif(-1,1)
#=================================================================
############ OTHER PARAMETERS OF INTEREST ############
#=================================================================
### INDEX TEST
#=================================================================
#### SUMMARY SENSITIVITY AND SPECIFICITY OF INDEX TEST
Summary_Se<-1/(1+exp(-mu[1]))
Summary_Sp<-1/(1+exp(-mu[2]))
#### BETWEEN_STUDY VARIANCE IN THE LOGIT(SENSITIVITY) AND LOGIT(SPECIFICITY)
tau.sq[1] <- pow(tau[1], 2)
tau.sq[2] <- pow(tau[2], 2)
#### BETWEEN_STUDY STANDARD DEVIATION IN THE LOGIT(SENSITIVITY) AND LOGIT(SPECIFICITY)
tau[1]<-pow(prec[1],-0.5)
tau[2]<-pow(prec[2],-0.5)
#### PREDICTED SENSITIVITY AND SPECIFICITY OF XPERT IN A FUTURE STUDY
Predicted.l[1:2] ~ dmnorm(mu[],T[,])
Predicted_Se <- 1/(1+exp(-Predicted.l[1]))
Predicted_Sp <- 1/(1+exp(-Predicted.l[2]))
#=================================================================
### REFERENCE TEST
#=================================================================
#### SUMMARY SENSITIVITY AND SPECIFICITY OF REFERENCE TEST
Summary_Se2<-1/(1+exp(-mu2[1]))
Summary_Sp2<-1/(1+exp(-mu2[2]))
#### BETWEEN_STUDY STANDARD DEVIATION IN THE LOGIT(SENSITIVITY) AND LOGIT(SPECIFICITY)
tau2[1] <-pow(prec2[1],-0.5)
tau2[2] <-pow(prec2[2],-0.5)
#### BETWEEN_STUDY VARIANCE IN THE LOGIT(SENSITIVITY) AND LOGIT(SPECIFICITY)
tau.sq2[1] <- pow(tau2[1], 2)
tau.sq2[2] <- pow(tau2[2], 2)
#### PREDICTED SENSITIVITY AND SPECIFICITY OF CULTURE IN A FUTURE STUDY
Predicted.l2[1:2] ~ dmnorm(mu2[],T2[,])
Predicted_Se2 <- 1/(1+exp(-Predicted.l2[1]))
Predicted_Sp2 <- 1/(1+exp(-Predicted.l2[2]))
}"
}else{
modelString =
"model {
#=================================================================
############ LIKELIHOOD ############
#=================================================================
for(i in 1:N) {
# The 4 cells in the two-by-two table of the new test vs. the imperfect reference standard in each study in the meta-analysis
cell[i,1:4] ~ dmulti(prob[i,1:4],n[i])
# Multinomial probabilities of the 4 cells of the two-by-two table expressed in terms of the disease prevalence (prev), the sensitivity (se1, se2) and specificity (sp1, sp2) of the two tests and the covariance between them among disease positive (covs12) and disease negative (covc12) groups
se[i] <- p[1,i]
sp[i] <- 1-p[2,i]
prob[i,1] <- prev[i]*( p[1,i] * se2[i] + covp[i] ) + (1-prev[i])*( p[2,i] *(1-sp2[i]) + covn[i] )
prob[i,2] <- prev[i]*( p[1,i] * (1-se2[i]) - covp[i] ) + (1-prev[i])*( p[2,i] *sp2[i] - covn[i] )
prob[i,3] <- prev[i]*( (1-p[1,i]) * se2[i] - covp[i] ) + (1-prev[i])*( (1-p[2,i]) *(1-sp2[i]) - covn[i] )
prob[i,4] <- prev[i]*( (1-p[1,i]) * (1-se2[i]) + covp[i] ) + (1-prev[i])*( (1-p[2,i]) *sp2[i] + covn[i] )
#=================================================================
############ CONDITIONAL DEPENDENCE ############
#=================================================================
#=======================================
# upper limits of covariance parameters
#=======================================
us[i]<-min(se[i],se2[i])-(se[i]*se2[i]);
uc[i]<-min(sp[i],sp2[i])-(sp[i]*sp2[i]);
ls[i]<- -(1-se[i])*(1-se2[i])
lc[i]<- -(1-sp[i])*(1-sp2[i])
#==============================================================
# prior distribution of transformed covariances on (0,1) range
#==============================================================
covp[i]<-0 #~dunif(ls[i],us[i]);
covn[i]<-0 #~dunif(lc[i],uc[i]);
#=================================================================
############ HIERARCHICAL PRIORS ############
#=================================================================
#=======================================
# Hierarchichal prior for xpert
#=======================================
logit(p[1, i]) <- l[i,1]
logit(p[2, i]) <- -l[i,2]
l[i,1:2] ~ dmnorm(mu[], T[,])
#=======================================
# Prior distribution on prevalence
#=======================================
prev[i] ~ dbeta(1,1)
}
# ==================================
# Hierarchical prior for CULTURE
# ==================================
for(j in 1:N) {
logit(se2[j]) <- l2[j,1]
logit(sp2[j]) <- l2[j,2]
l2[j,1:2] ~ dmnorm(mu2[1:2], T2[1:2,1:2])
}
#=================================================================
############ HYPER PRIOR DISTRIBUTIONS ################
#=================================================================
### INDEX TEST
#=================================================================
### prior for the logit transformed sensitivity (mu[1]) and specificity (mu[2])
mu[1] ~ dnorm(0,0.25)
mu[2] ~ dnorm(0,0.25)
T[1:2,1:2]<-inverse(TAU[1:2,1:2])
#### BETWEEN-STUDY VARIANCE-COVARIANCE MATRIX
TAU[1,1] <- tau[1]*tau[1]
TAU[2,2] <- tau[2]*tau[2]
TAU[1,2] <- rho*tau[1]*tau[2]
TAU[2,1] <- rho*tau[1]*tau[2]
#### prec = between-study precision in the logit(sensitivity) and logit(specificity)
prec[1] ~ dgamma(2,0.5)
prec[2] ~ dgamma(2,0.5)
rho ~ dunif(-1,1)
#=================================================================
### REFERENCE TEST
#=================================================================
### prior for the logit transformed sensitivity (mu2[1]) and specificity (mu2[2])
mu2[1] ~ dnorm(0,0.25)
mu2[2] ~ dnorm(0,0.25)
T2[1:2,1:2]<-inverse(TAU2[1:2,1:2])
#### BETWEEN-STUDY VARIANCE-COVARIANCE MATRIX
TAU2[1,1] <- tau2[1]*tau2[1]
TAU2[2,2] <- tau2[2]*tau2[2]
TAU2[1,2] <- rho2*tau2[1]*tau2[2]
TAU2[2,1] <- rho2*tau2[1]*tau2[2]
#### prec = between-study precision in the logit(sensitivity) and logit(specificity)
prec2[1] ~ dgamma(2,0.5)
prec2[2] ~ dgamma(2,0.5)
rho2 ~ dunif(-1,1)
#=================================================================
############ OTHER PARAMETERS OF INTEREST ############
#=================================================================
### INDEX TEST
#=================================================================
#### SUMMARY SENSITIVITY AND SPECIFICITY OF INDEX TEST
Summary_Se<-1/(1+exp(-mu[1]))
Summary_Sp<-1/(1+exp(-mu[2]))
#### BETWEEN_STUDY VARIANCE IN THE LOGIT(SENSITIVITY) AND LOGIT(SPECIFICITY)
tau.sq[1] <- pow(tau[1], 2)
tau.sq[2] <- pow(tau[2], 2)
#### BETWEEN_STUDY STANDARD DEVIATION IN THE LOGIT(SENSITIVITY) AND LOGIT(SPECIFICITY)
tau[1]<-pow(prec[1],-0.5)
tau[2]<-pow(prec[2],-0.5)
#### PREDICTED SENSITIVITY AND SPECIFICITY OF XPERT IN A FUTURE STUDY
Predicted.l[1:2] ~ dmnorm(mu[],T[,])
Predicted_Se <- 1/(1+exp(-Predicted.l[1]))
Predicted_Sp <- 1/(1+exp(-Predicted.l[2]))
#=================================================================
### REFERENCE TEST
#=================================================================
#### SUMMARY SENSITIVITY AND SPECIFICITY OF REFERENCE TEST
Summary_Se2<-1/(1+exp(-mu2[1]))
Summary_Sp2<-1/(1+exp(-mu2[2]))
#### BETWEEN_STUDY STANDARD DEVIATION IN THE LOGIT(SENSITIVITY) AND LOGIT(SPECIFICITY)
tau2[1] <-pow(prec2[1],-0.5)
tau2[2] <-pow(prec2[2],-0.5)
#### BETWEEN_STUDY VARIANCE IN THE LOGIT(SENSITIVITY) AND LOGIT(SPECIFICITY)
tau.sq2[1] <- pow(tau2[1], 2)
tau.sq2[2] <- pow(tau2[2], 2)
#### PREDICTED SENSITIVITY AND SPECIFICITY OF CULTURE IN A FUTURE STUDY
Predicted.l2[1:2] ~ dmnorm(mu2[],T2[,])
Predicted_Se2 <- 1/(1+exp(-Predicted.l2[1]))
Predicted_Sp2 <- 1/(1+exp(-Predicted.l2[2]))
}"
}The posterior samples were obtained by running a latent-class meta-analysis model (Xie, Sinclair and Dendukuri(2017)) with 3 independent chains each having their own starting values to assess convergence of the MCMC algorithm. For each chain, after discarding the first 100 iterations (burn-in), we kept the next 100 iterations to form a posterior samples of 300 iterations.
** Prior Distributions**
A hierarchical prior distribution structure is specified for the sensitivity and specificity of the index test. The prior distributions are as followed
- \(mu[1] \sim N(\mu=0,\sigma^2=4)\)
- \(mu[2] \sim N(\mu=0,\sigma^2=4)\)
- \(prec[1] \sim \Gamma(\alpha=2,s=\frac{1}{2})\) where \(\alpha\) and \(s\) are the shape and scale parameters respectively
- \(prec[2] \sim \Gamma(\alpha=2,s=\frac{1}{2})\) where \(\alpha\) and \(s\) are the shape and scale parameters respectively
- \(rho \sim U(-1,1)\)
A similar hierarchical prior distribution is specified over the sensitivity and specificity of the reference standard. The prior distributions are as followed
- \(mu2[1] \sim N(\mu=0,\sigma^2=4)\)
- \(mu2[2] \sim N(\mu=0,\sigma^2=4)\)
- \(prec2[1] \sim \Gamma(\alpha=2,s=\frac{1}{2})\) where \(\alpha\) and \(s\) are the shape and scale parameters respectively
- \(prec2[2] \sim \Gamma(\alpha=2,s=\frac{1}{2})\) where \(\alpha\) and \(s\) are the shape and scale parameters respectively
- \(rho2 \sim U(-1,1)\)
Additional prior distributions must be specified for the prevalence in each study as followed
- \(prev \sim \beta(1,1)\), for \(i \in 1, ..., n\) where \(n\) is the number of studies in the meta-analysis
** Seed value for reproducibility : ** 616
POSTERIOR RESULTS
Posterior mean, standard deviation (sd) as well as posterior median (50%) and the 95% credible interval (2.5% and 97.5%) statistics are presented below. Convergence statistics are also provided.
Rhatis the Gelman-Rubin statistic (Gelman and Ruben(1992), Brooks and Gelman(1998)). It is enabled when 2 or more chains are generated. It evaluates MCMC convergence by comparing within- and between-chain variability for each model parameter.Rhattends to 1 as convergence is approached.n.effis the effective sample size (Gelman et al(2013). Because the MCMC process causes the posterior draws to be correlated, the effective sample size is an estimate of the sample size required to achieve the same level of precision if that sample was a simple random sample. When draws are correlated, the effective sample size will generally be lower than the actual numbers of draws resulting in poor posterior estimates.
Posterior estimates are provided for the following parameters :
Parameters of index test
- Predicted sensitivity of index test in a future sutdy, noted as Predicted_Se
- Predicted specificity in a future study, noted as Predicted_Sp
- Summary sensitivity across all studies, noted as Summary_Se
- Summary specificity across all studies, noted as Summary_Sp
- Mean logit-transformed sensitivity, noted as mu[1]
- Mean logit-transformed sensitivity, noted as mu[2]
- Correlation between the mean logit-transformed sensitivity and the mean logit-transformed specificity, noted as rho
- Sensitivity in individual studies, noted as se[i], where i is the study identifier
- Specificity in individual studies, noted as sp[i], where i is the study identifier
- Between-study standard deviation in the logit-transformed sensitivity, noted as tau[1]
- Between-study standard deviation in the logit-transformed specificity, noted as tau[2]
- Between-study variance in the logit-transformed sensitivity, noted as tau.sq[1]
- Between-study variance in the logit-transformed specificity, noted as tau.sq[2]
Parameters of reference test
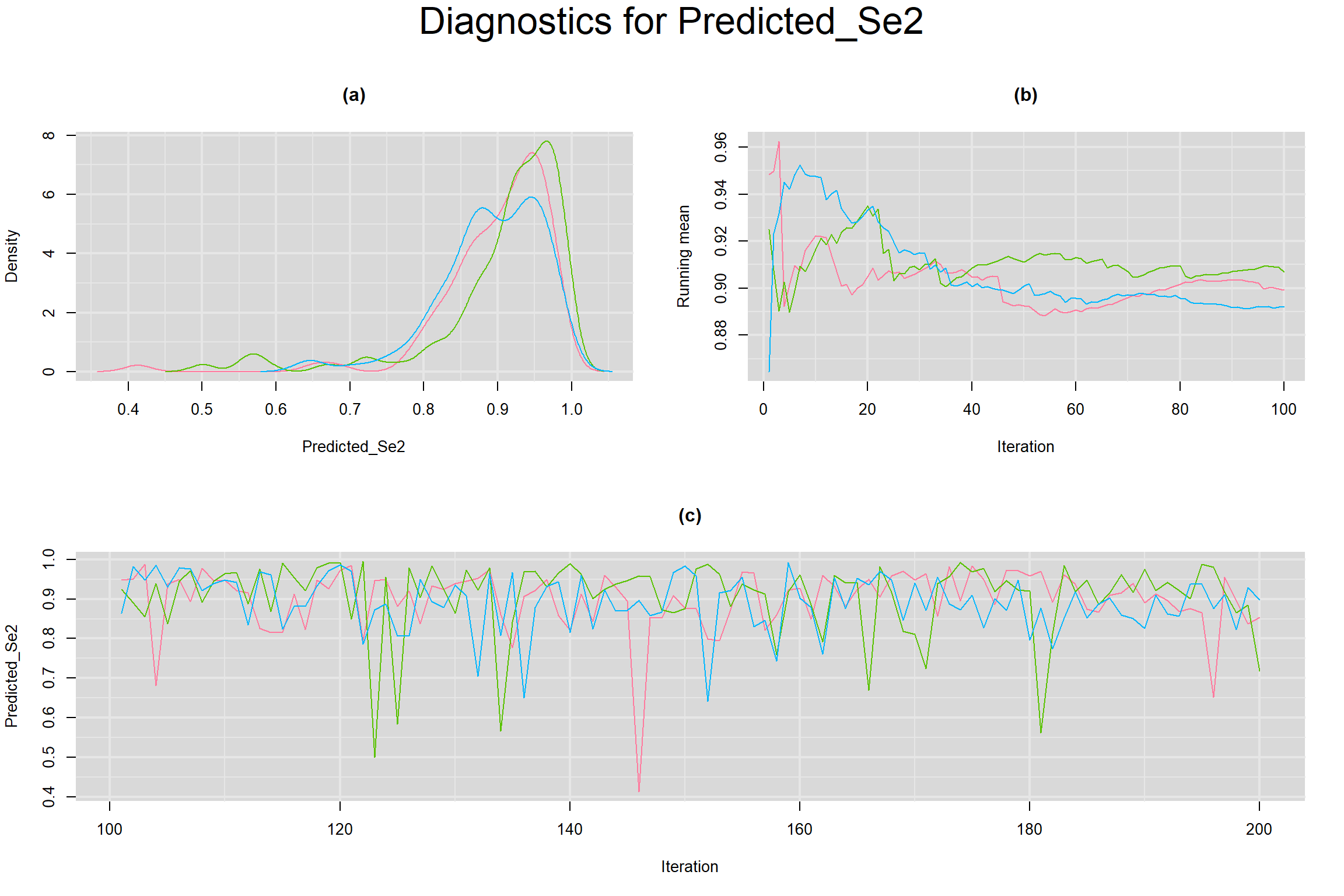
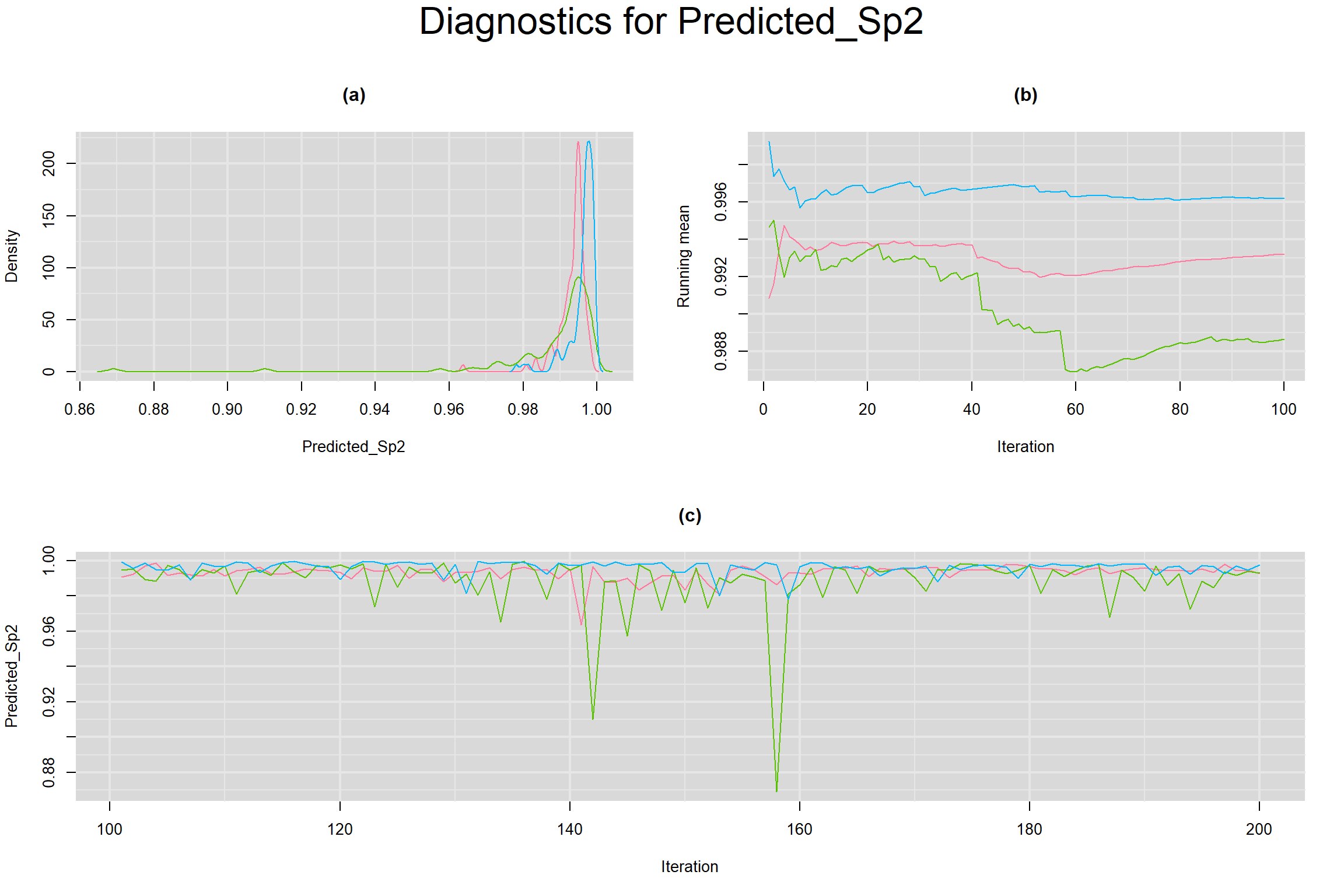
- Predicted sensitivity in a future sutdy, noted as Predicted_Se2
- Predicted specificity in a future study, noted as Predicted_Sp2
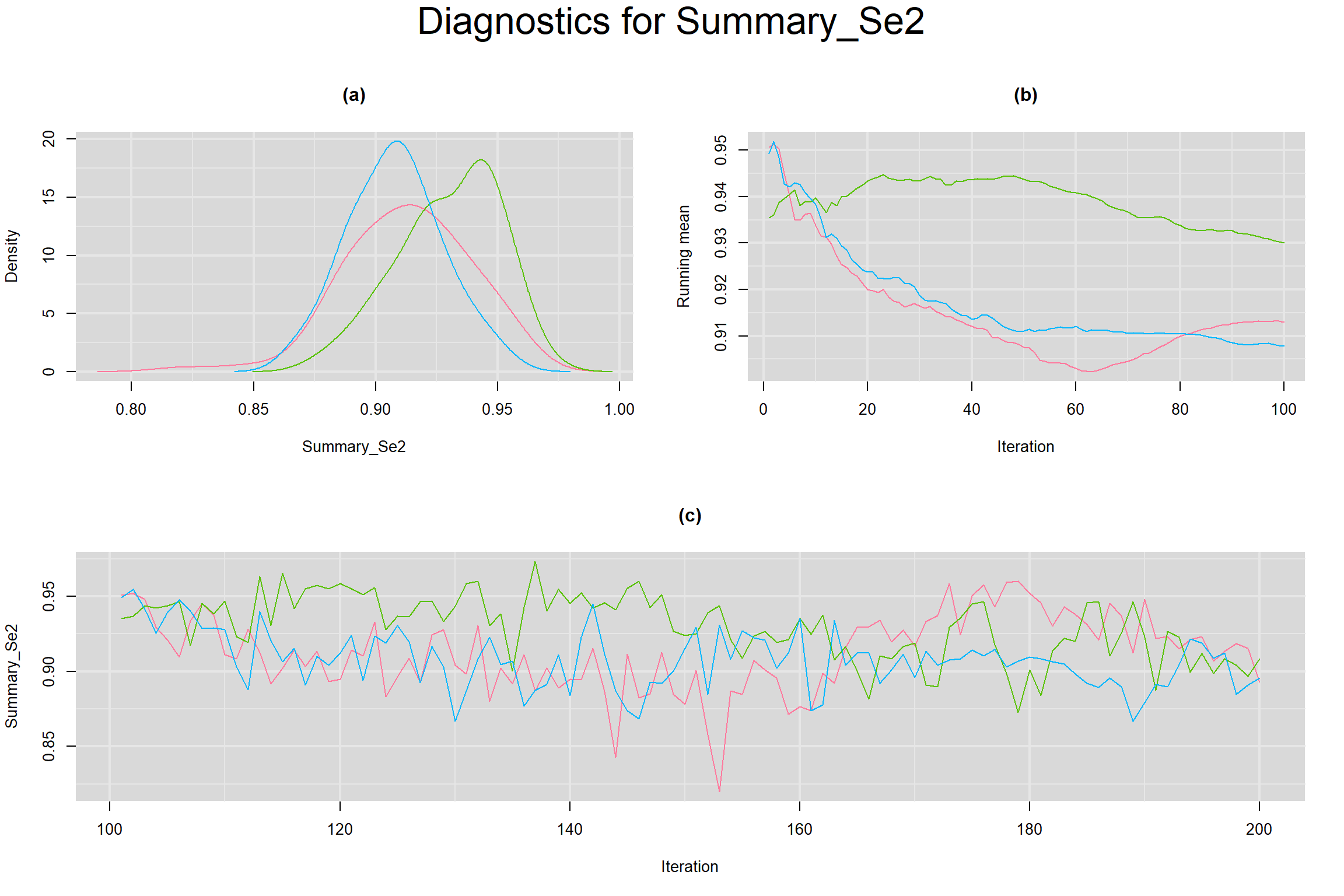
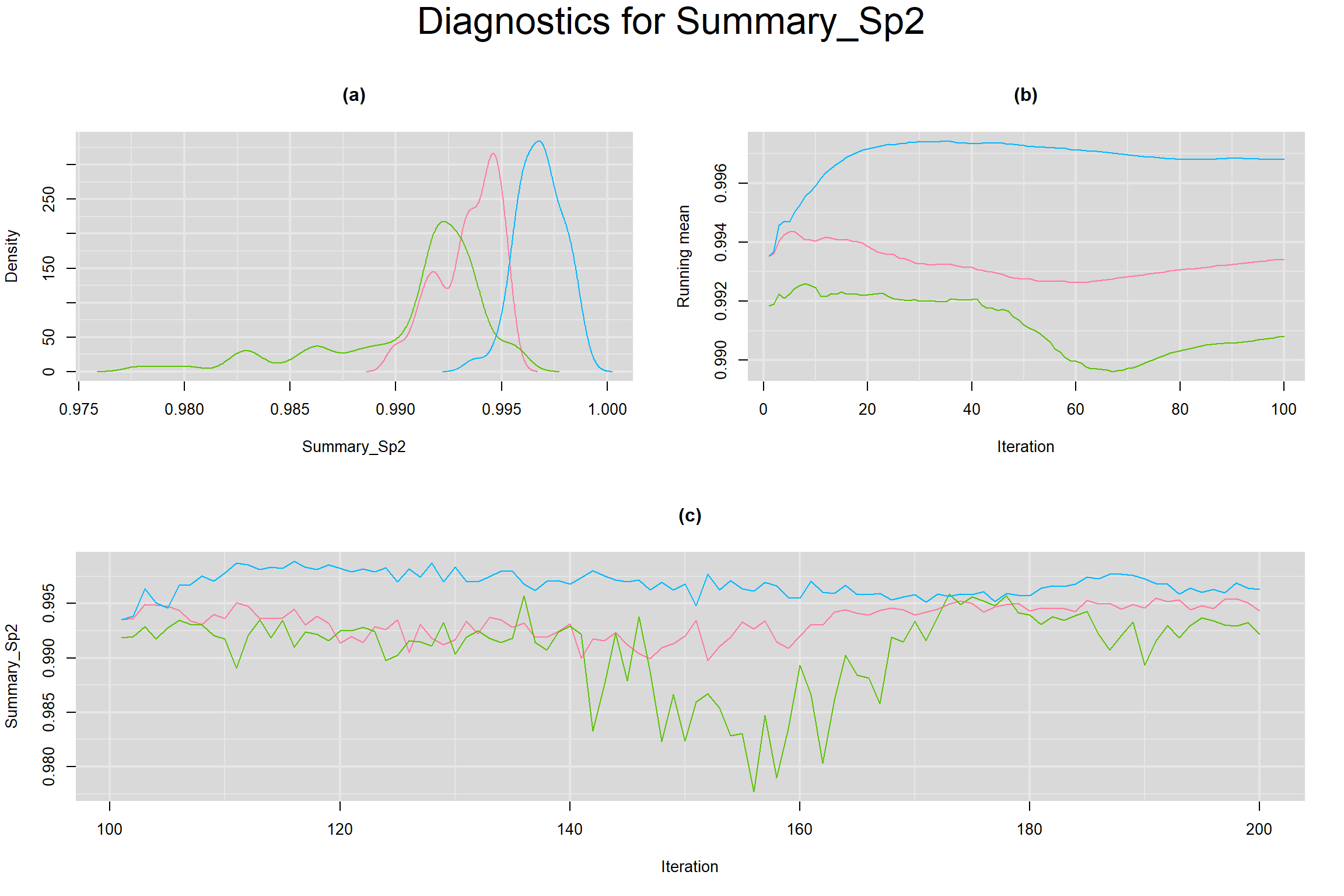
- Summary sensitivity across all studies, noted as Summary_Se2
- Summary specificity across all studies, noted as Summary_Sp2
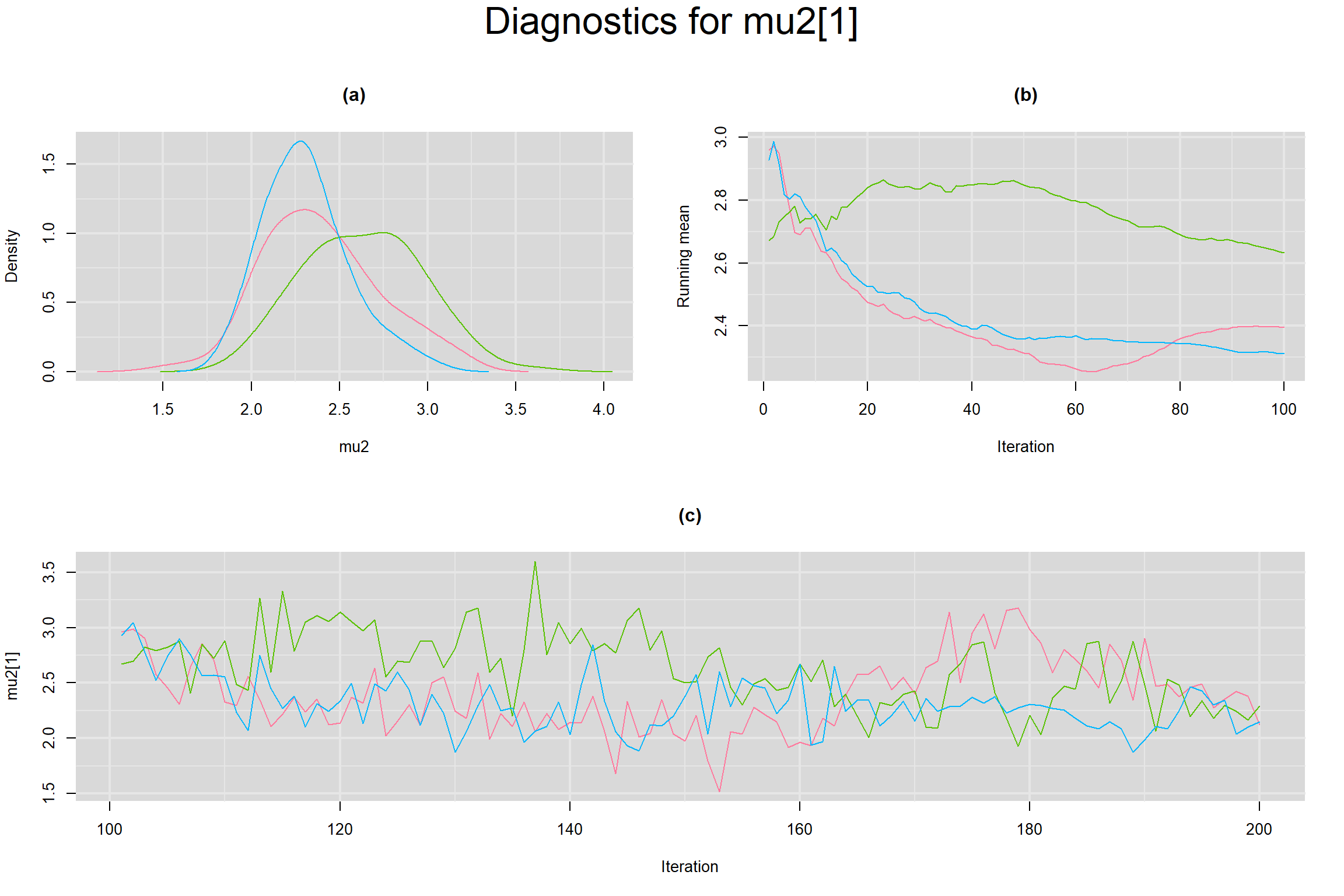
- Mean logit-transformed sensitivity, noted as mu2[1]
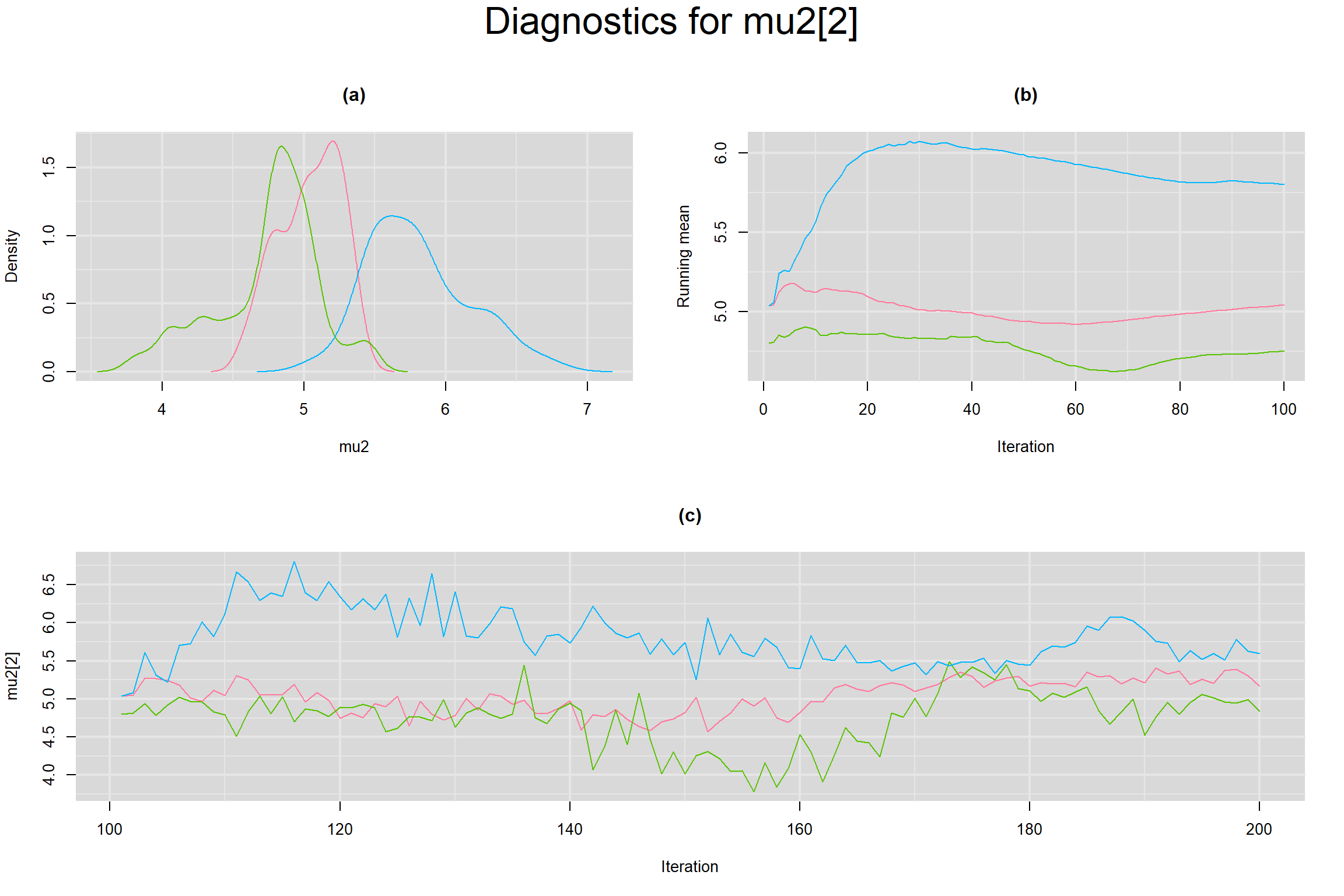
- Mean logit-transformed sensitivity, noted as mu2[2]
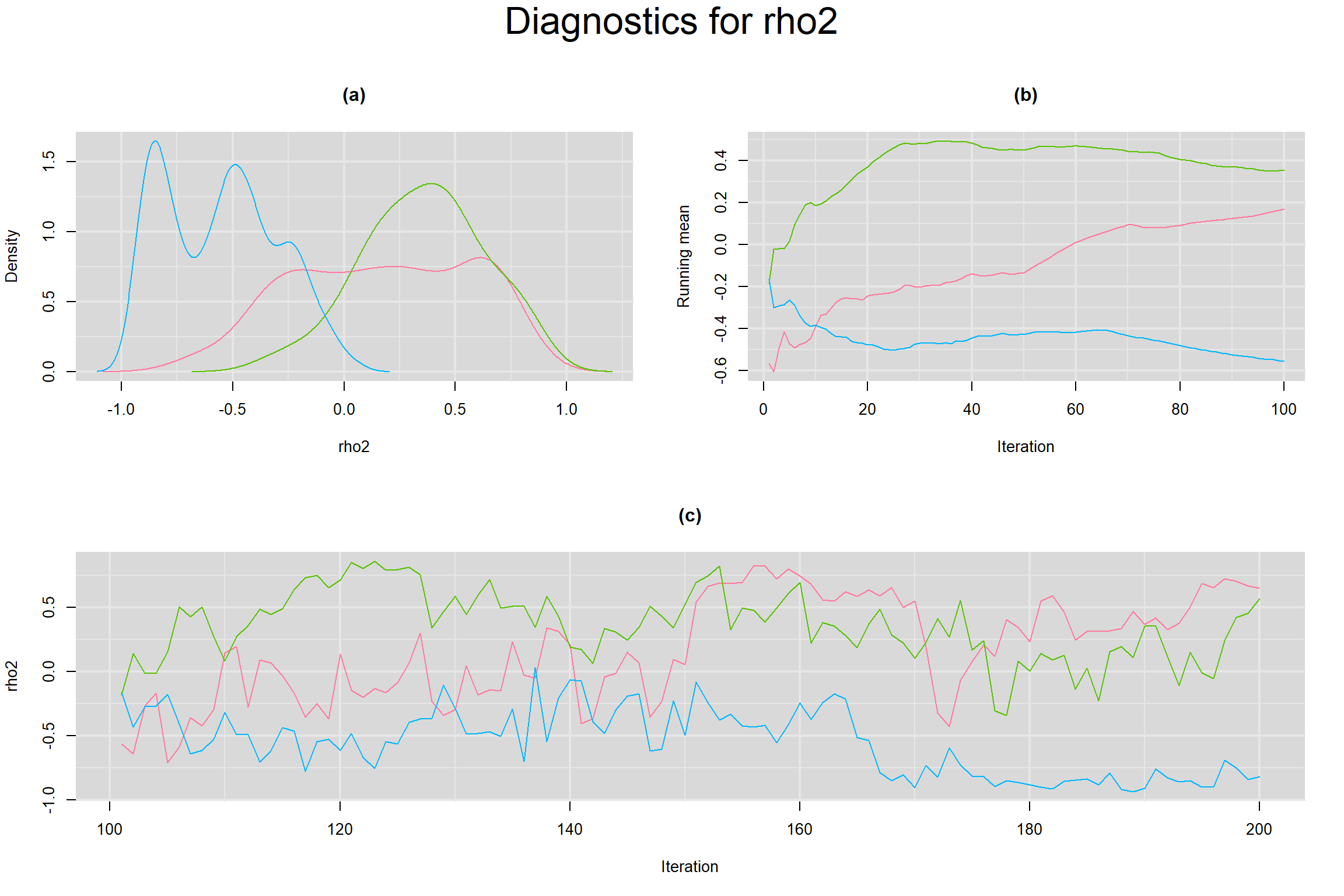
- Correlation between the mean logit-transformed sensitivity and the mean logit-transformed specificity, noted as rho2
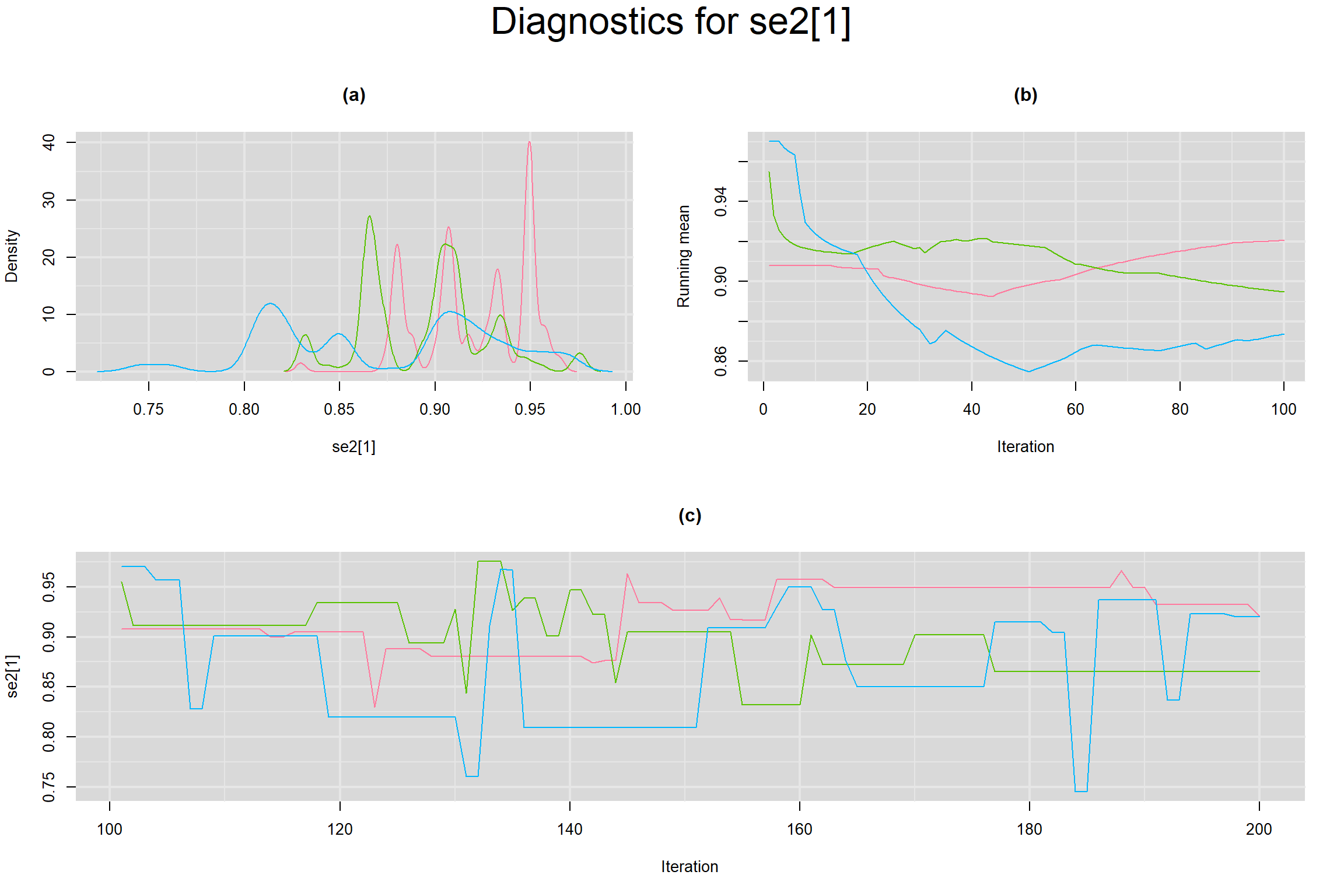
- Sensitivity in individual studies, noted as se2[i], where i is the study identifier
- Specificity in individual studies, noted as sp2[i], where i is the study identifier
- Between-study standard deviation in the logit-transformed sensitivity, noted as tau2[1]
- Between-study standard deviation in the logit-transformed specificity, noted as tau2[2]
- Between-study variance in the logit-transformed sensitivity, noted as tau.sq2[1]
- Between-study variance in the logit-transformed specificity, noted as tau.sq2[2]
Other parameters
- Prevalence in each study, noted as prev
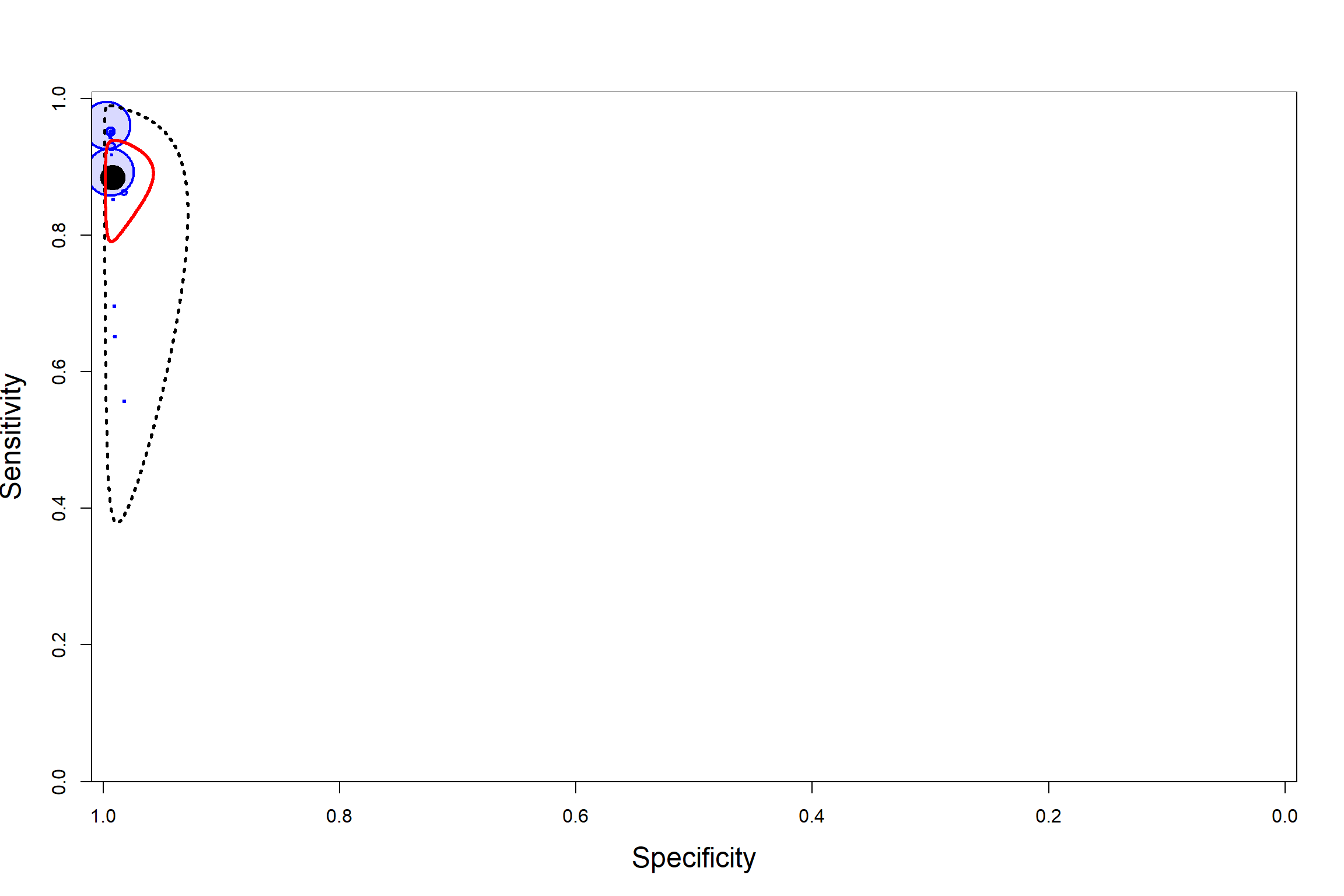
POSTERIOR ESTIMATES NEEDED TO CREATE SROC PLOT IN RevMan
The following posterior estimates are required in order to create the SROC plot in RevMan :
- E(logitSe) : Mean logit-transformed sensitivity, mu[1] = 2.0426
- E(logitSp) : Mean logit-transformed sensitivity, mu[2] = 5.0932
- Var(logitSe) : Between-study variance in the logit-transformed sensitivity, tau.sq[1] = 1.0728
- Var(logitSp) : Between-study variance in the logit-transformed specificity, tau.sq[2] = 2.1072
- Corr(logits) : Correlation between the mean logit-transformed sensitivity and the mean logit-transformed specificity, rho = 0.3208
- Cov(Es) : Covariance between the posterior samples of the mean logit-transformed sensitivity and mean logit-transformed specificity, -0.0195
- SE(E(logitSe)) : Estimated standard error of mean logit-transformed sensitivity = 0.2879
- SE(E(logitSp)) : Estimated standard error of mean logit-transformed specificity = 0.7083
SUMMARY ROC PLOT
CONVERGENCE DIAGNOSTIC TOOLS
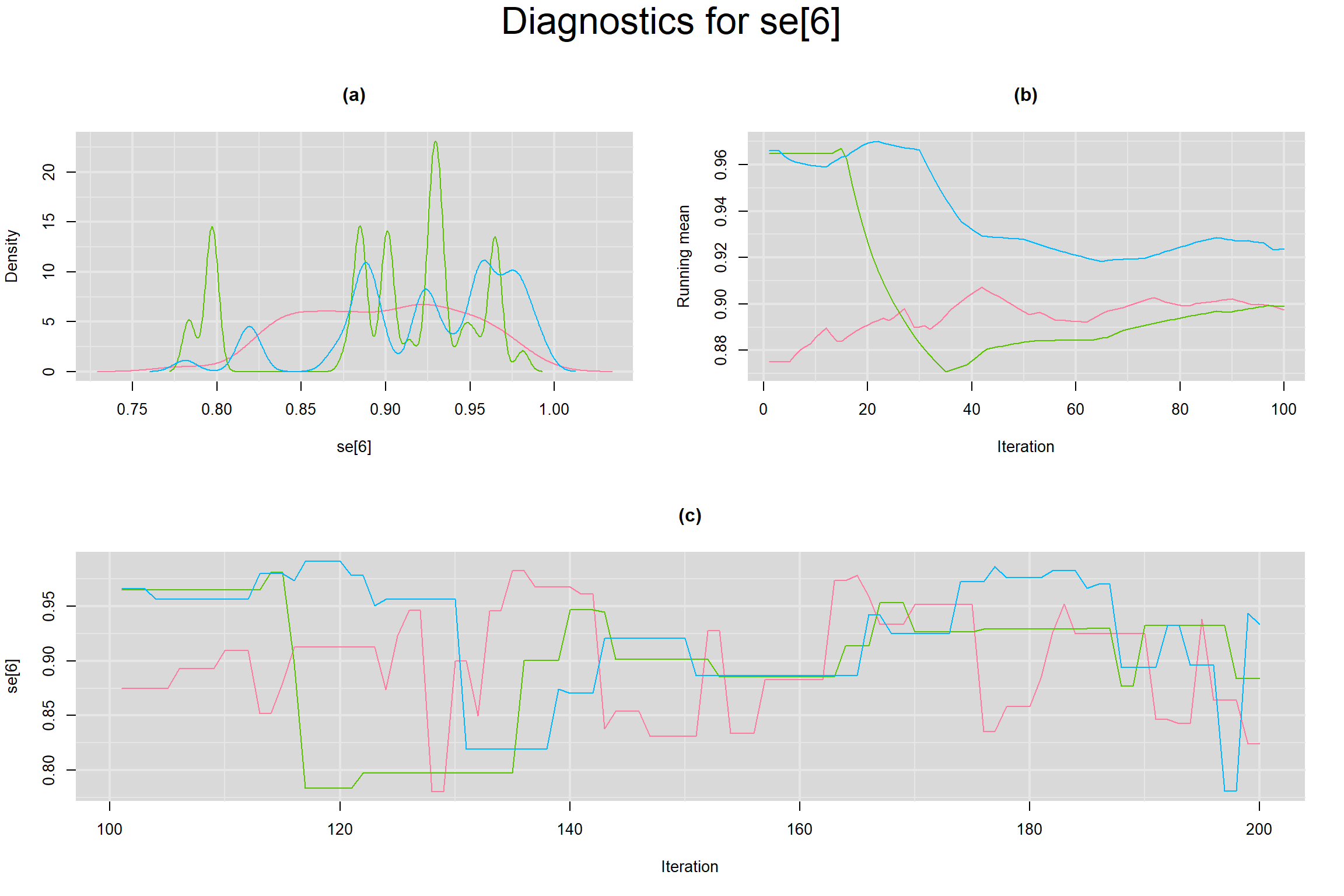
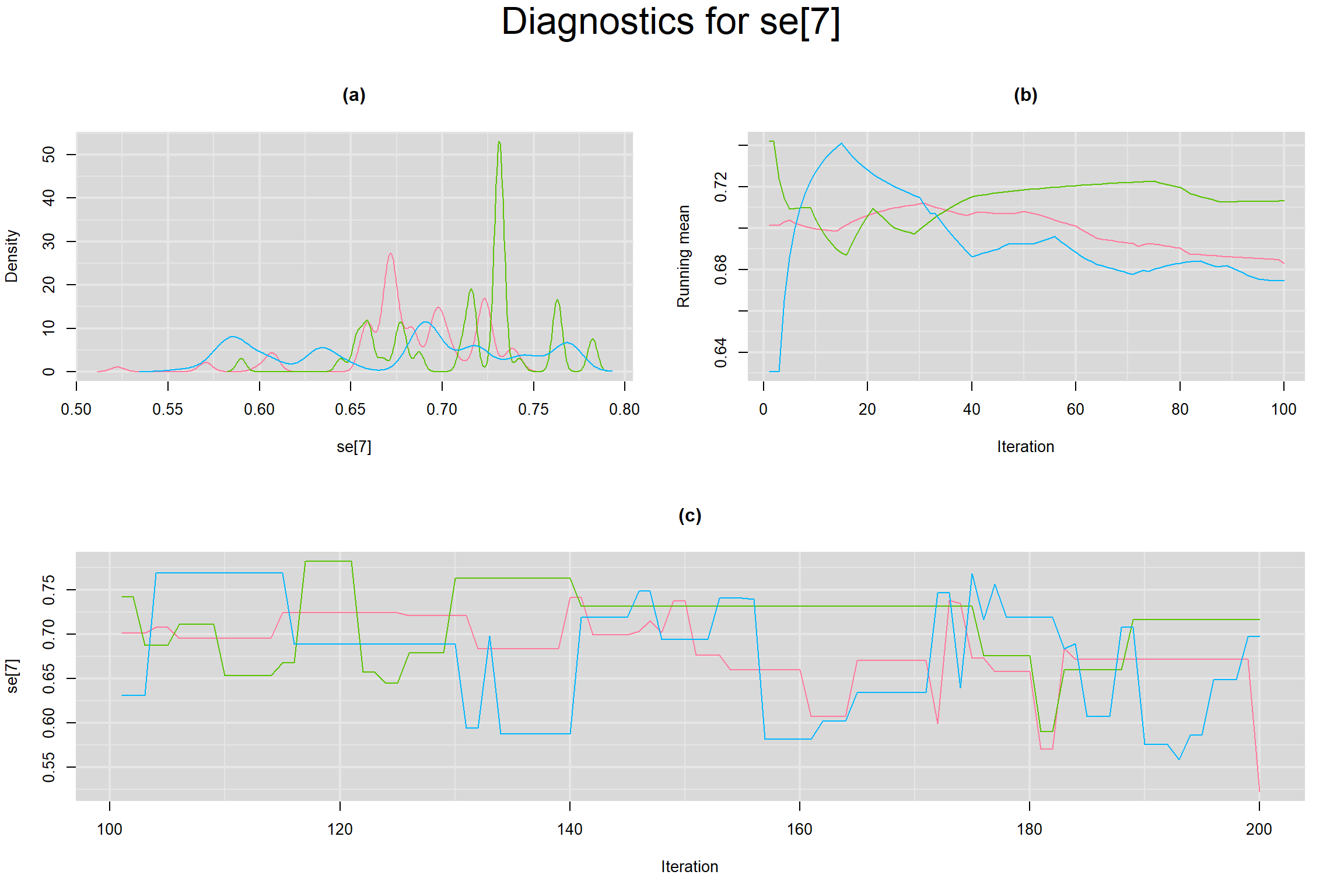
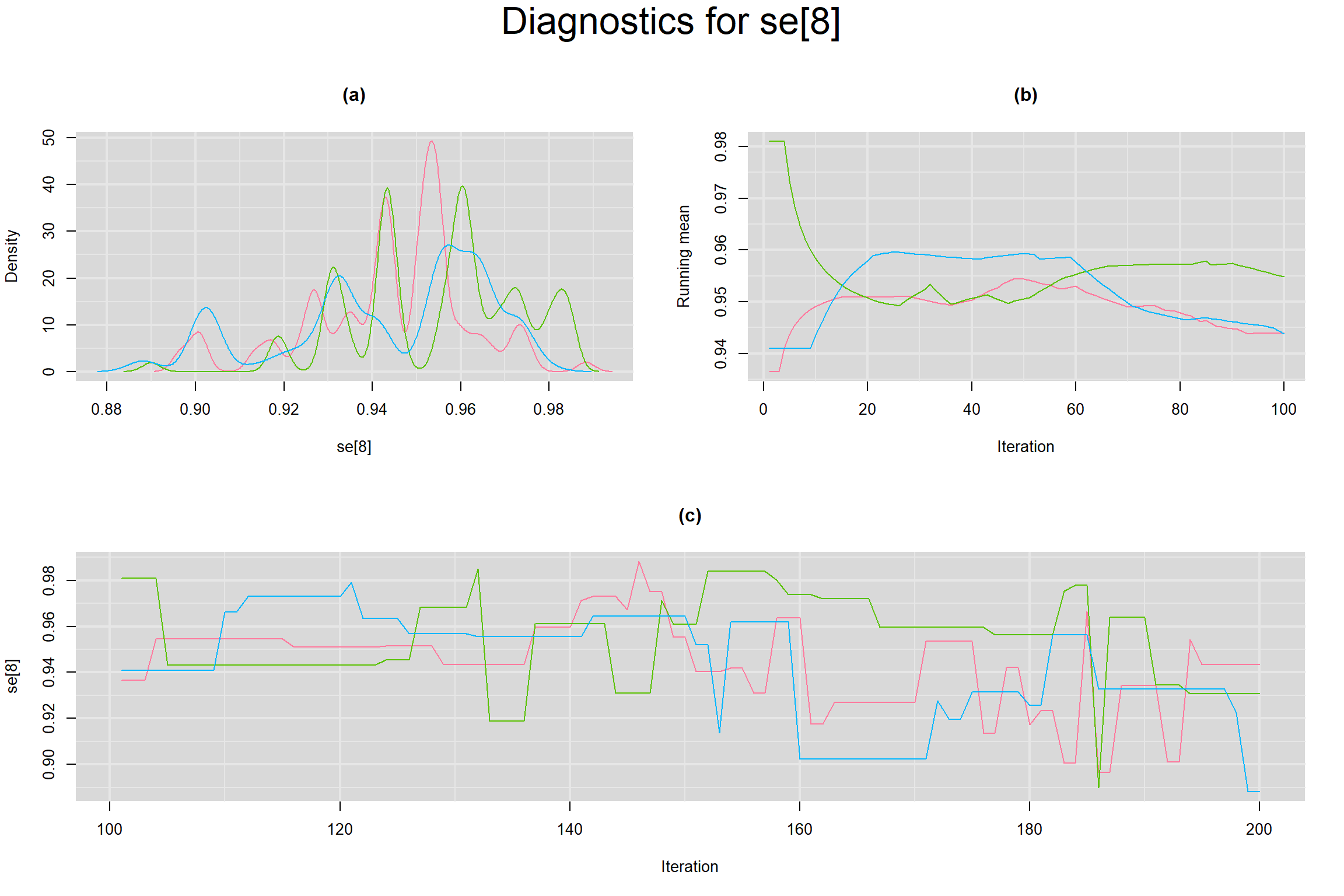
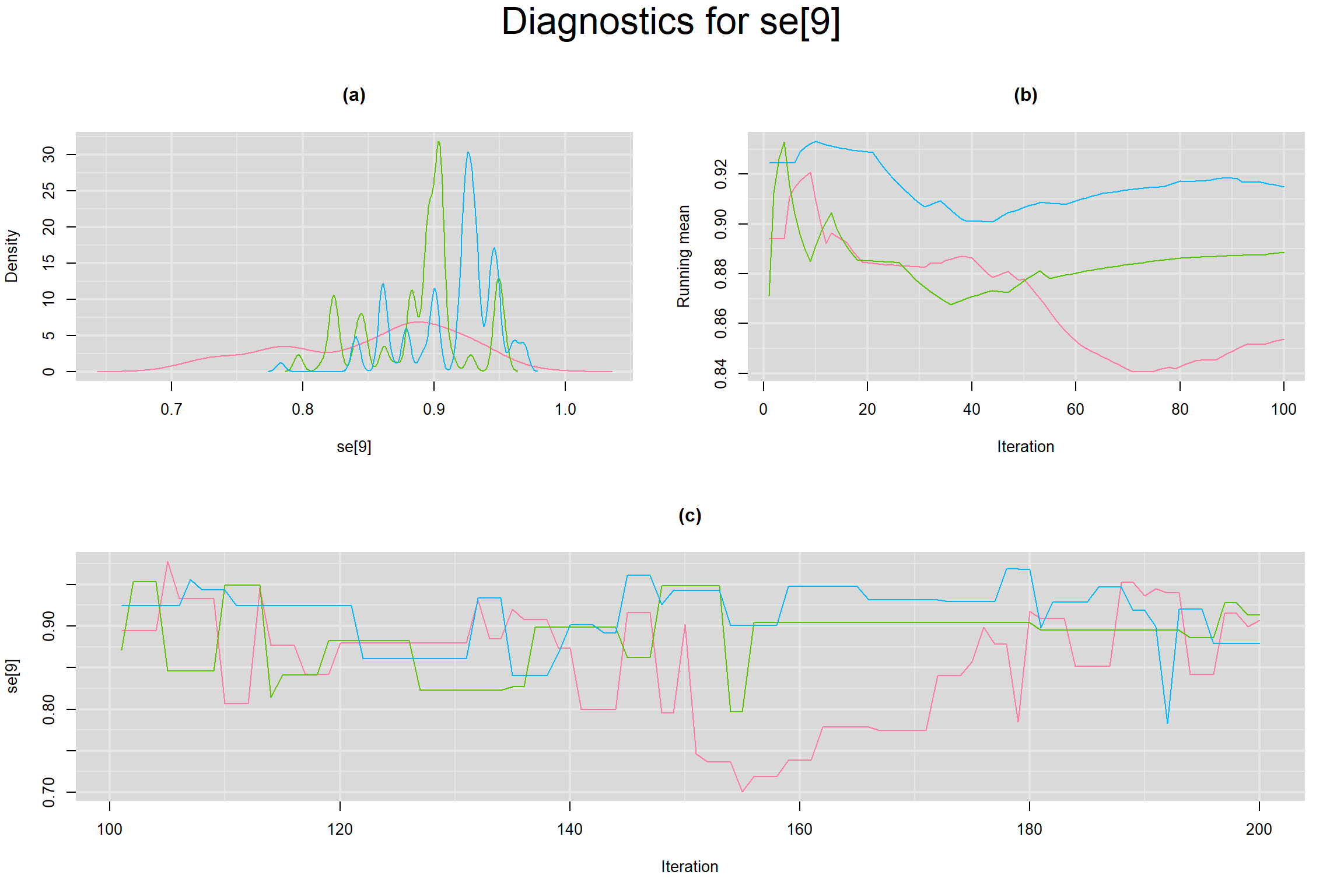
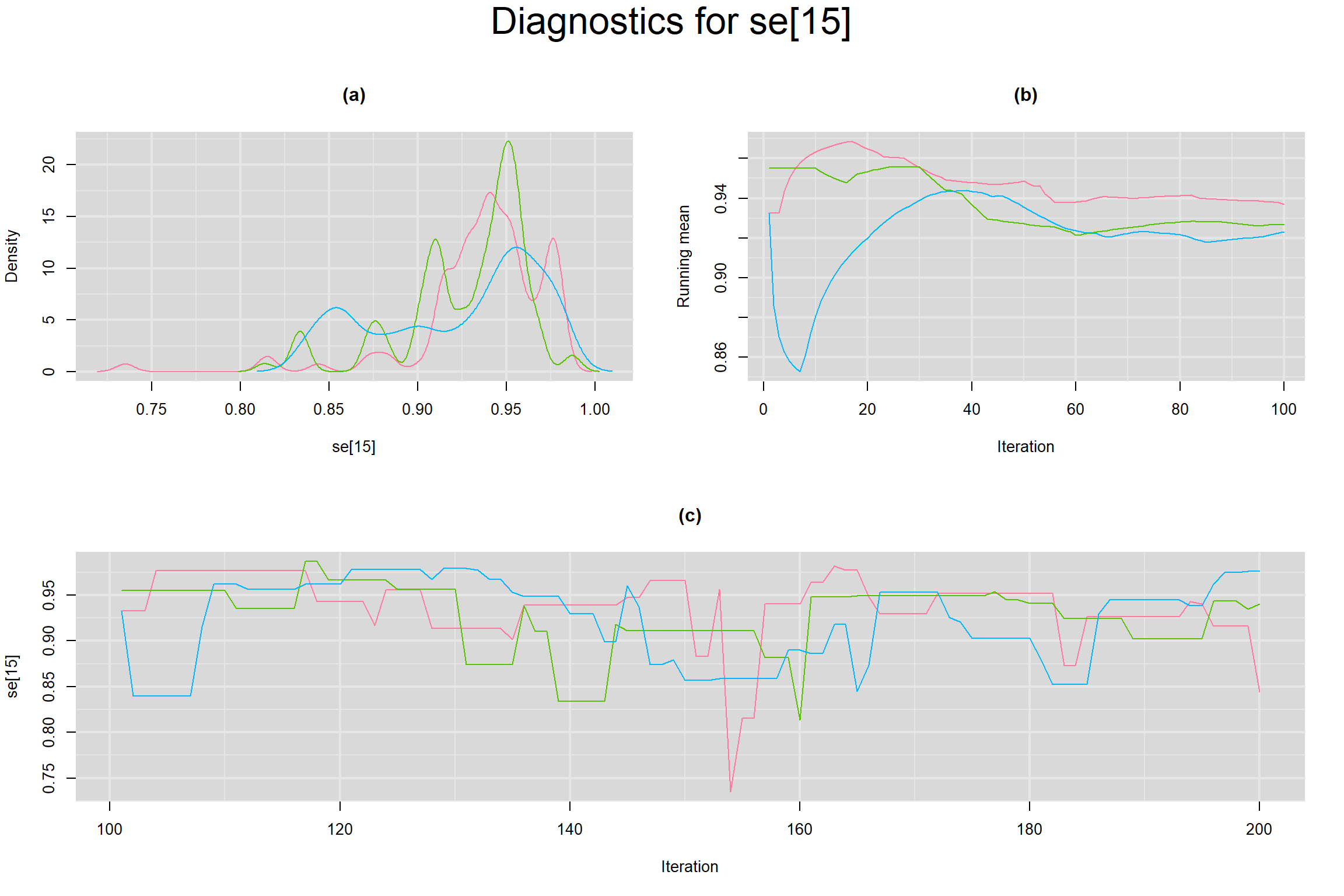
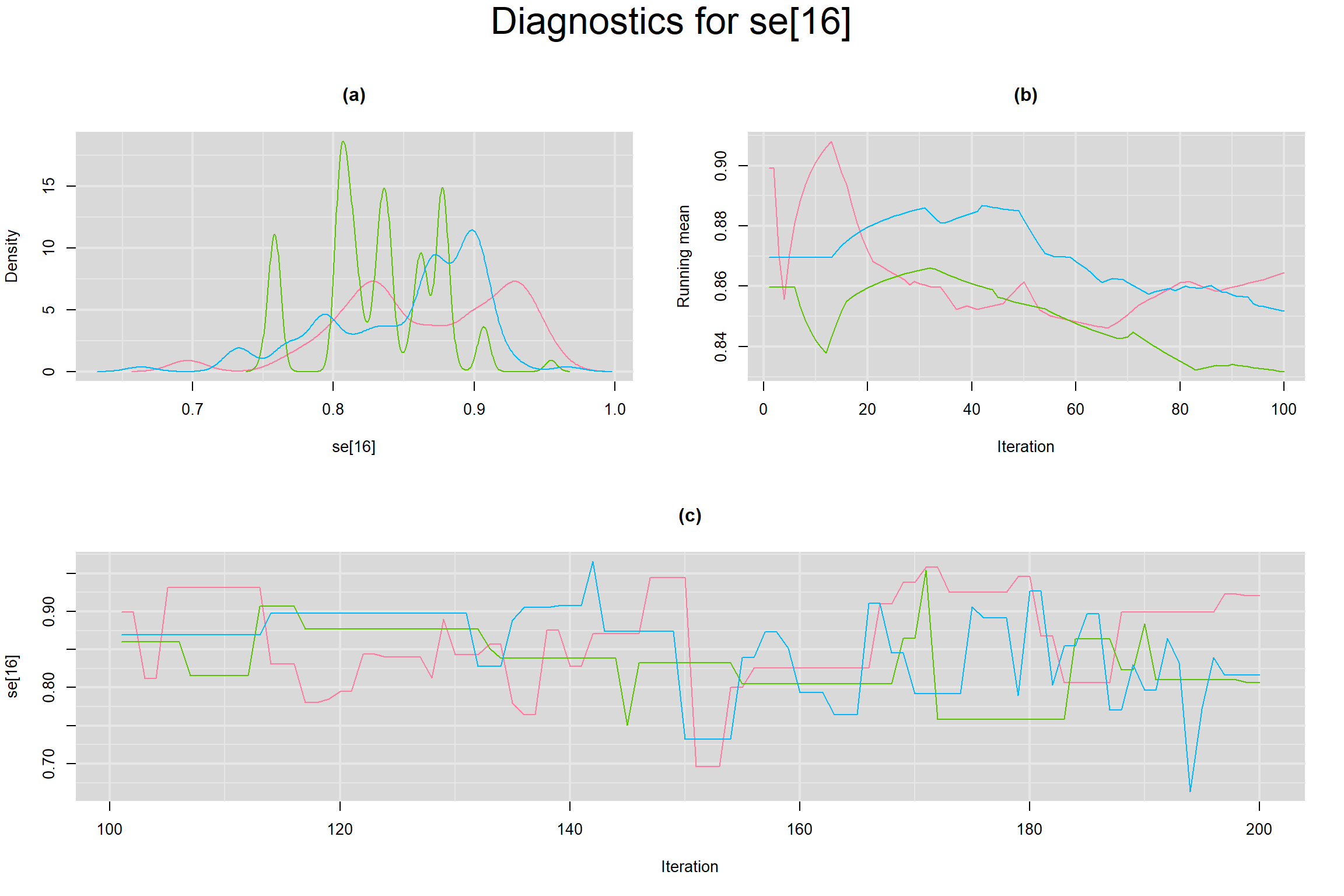
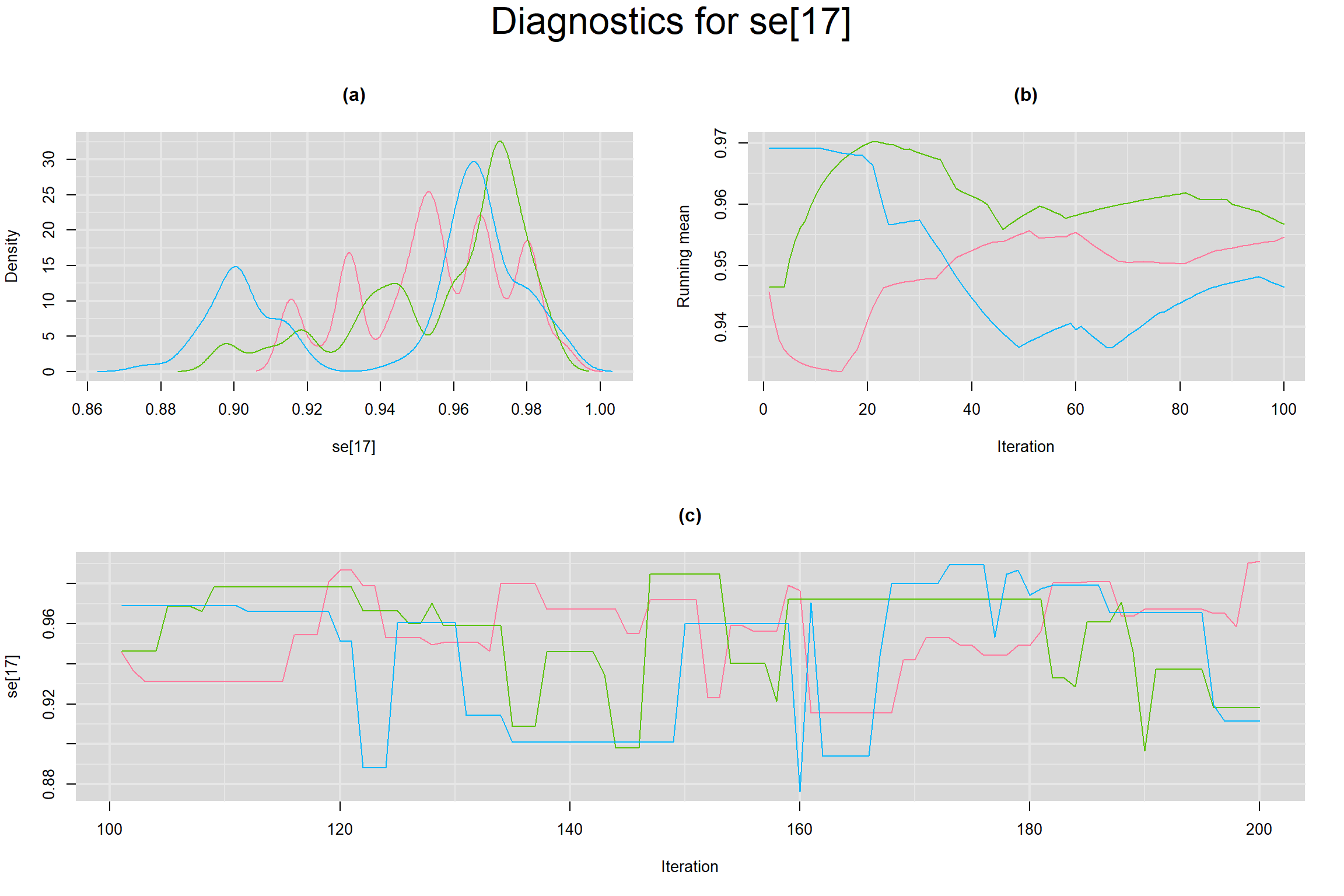
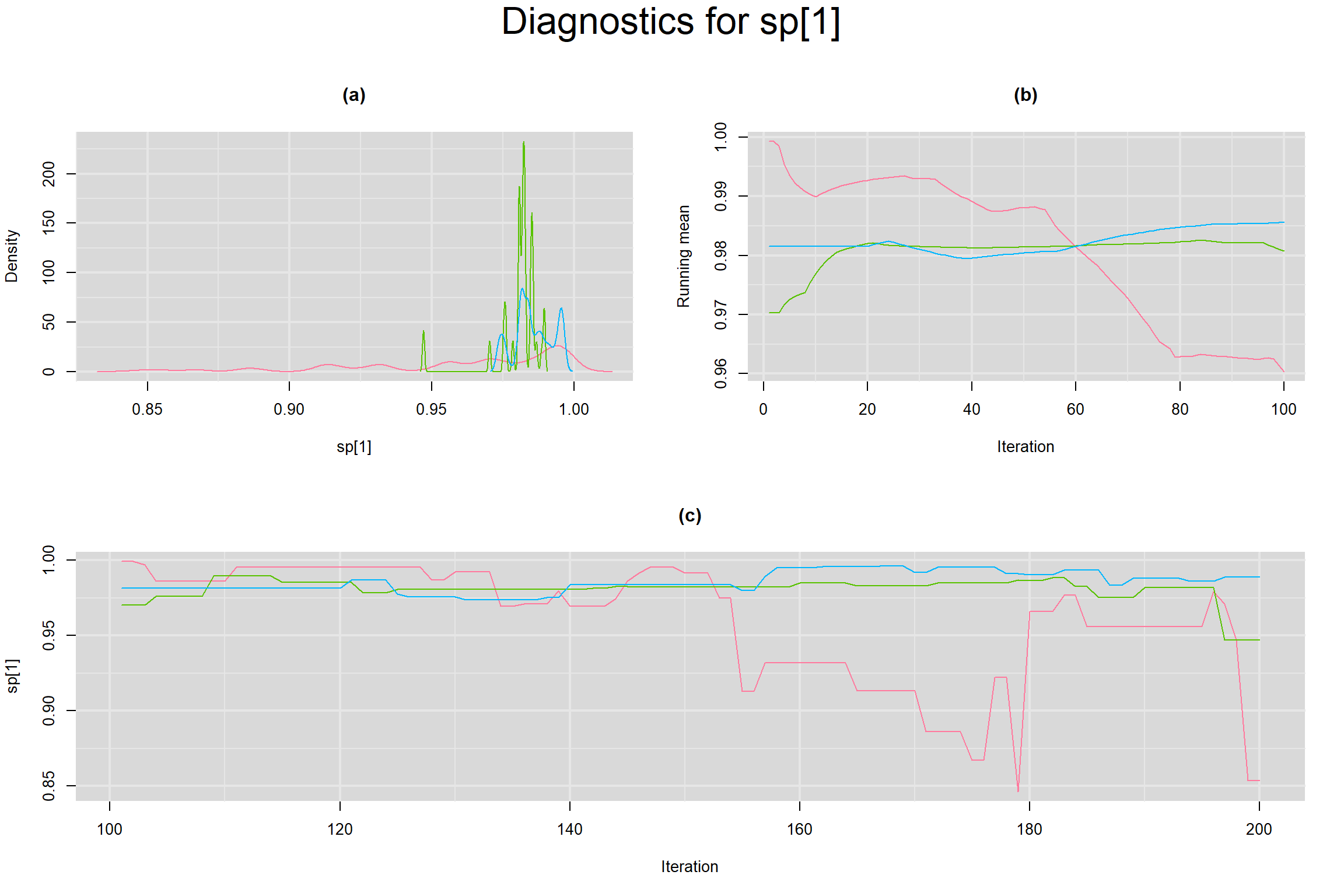
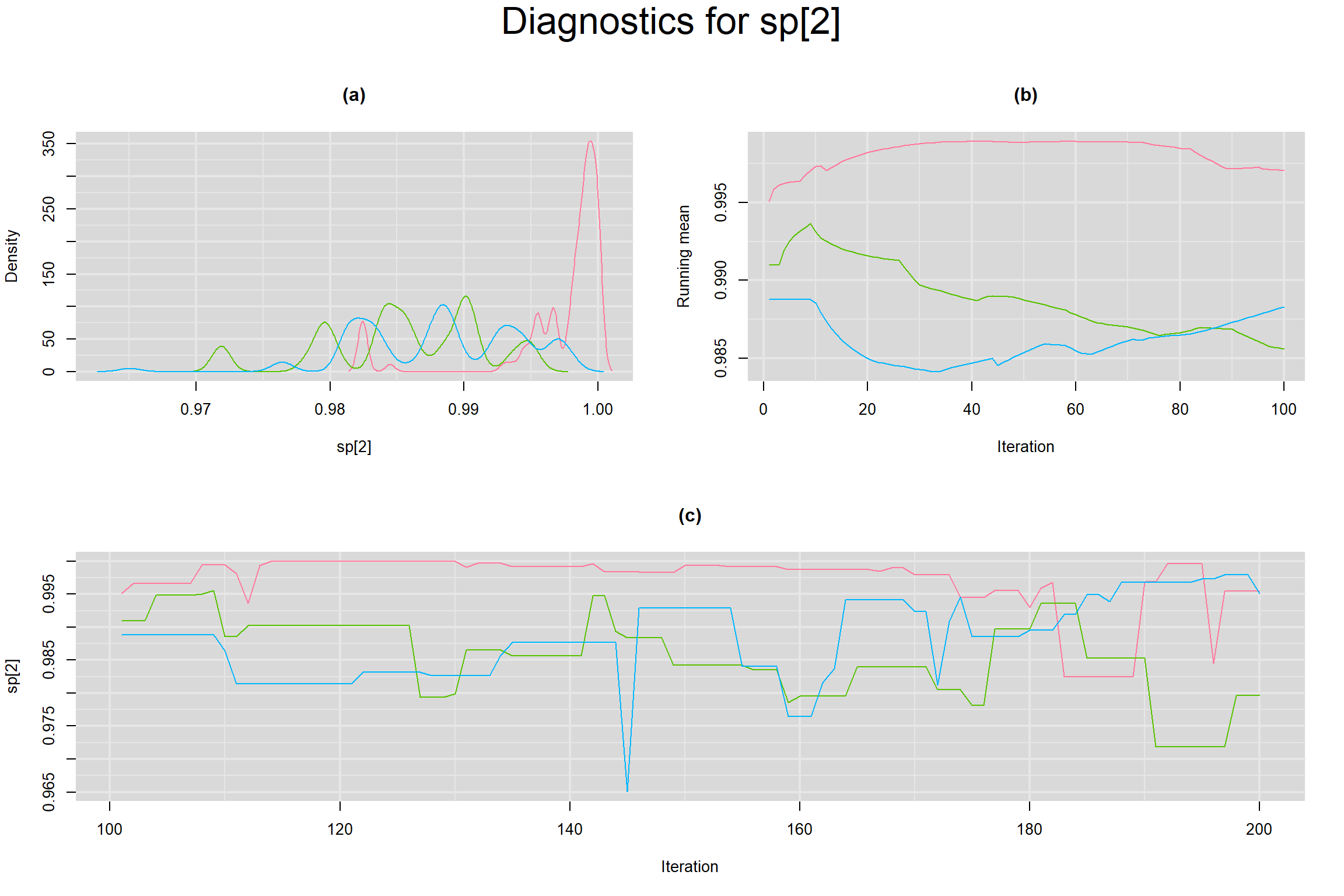
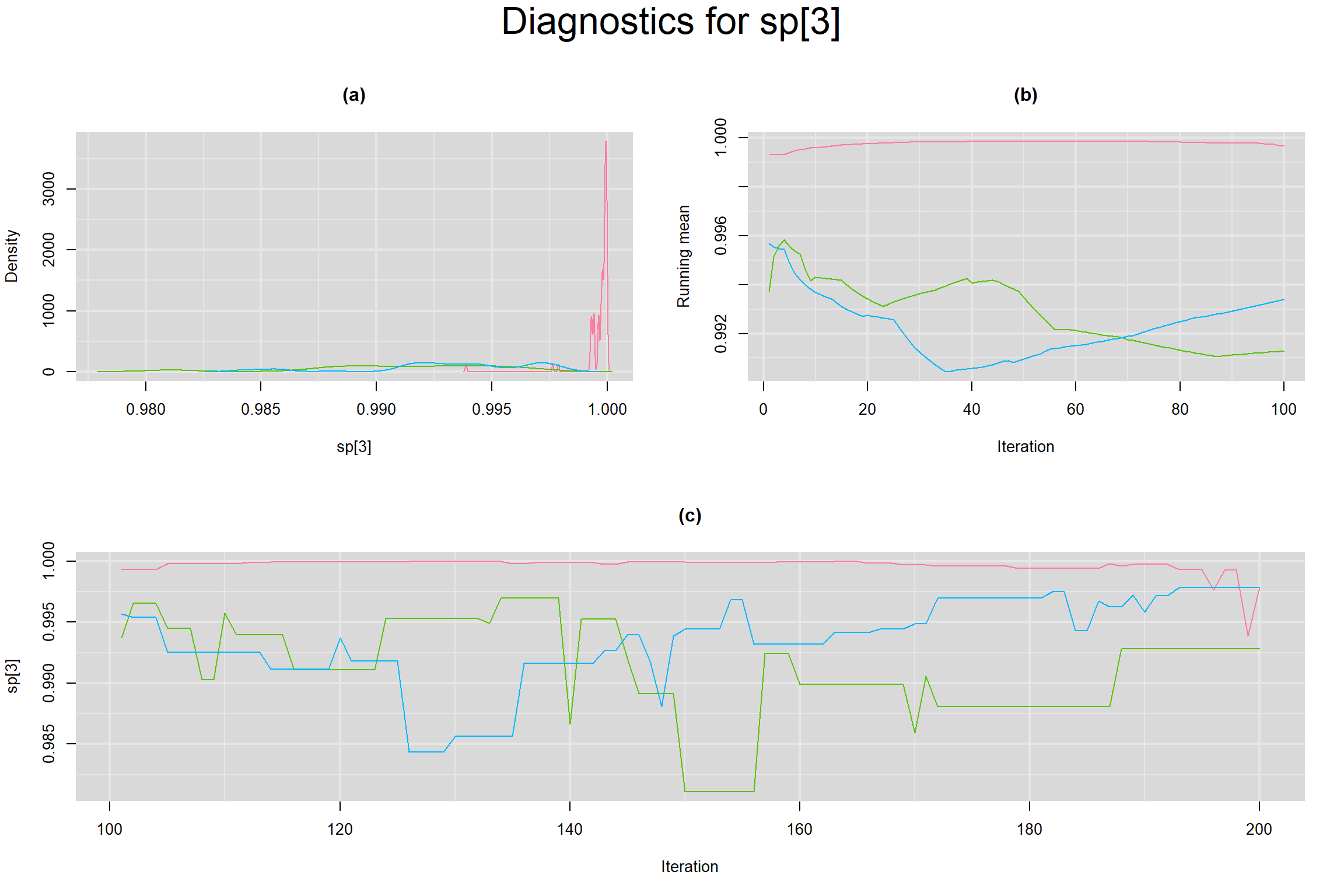
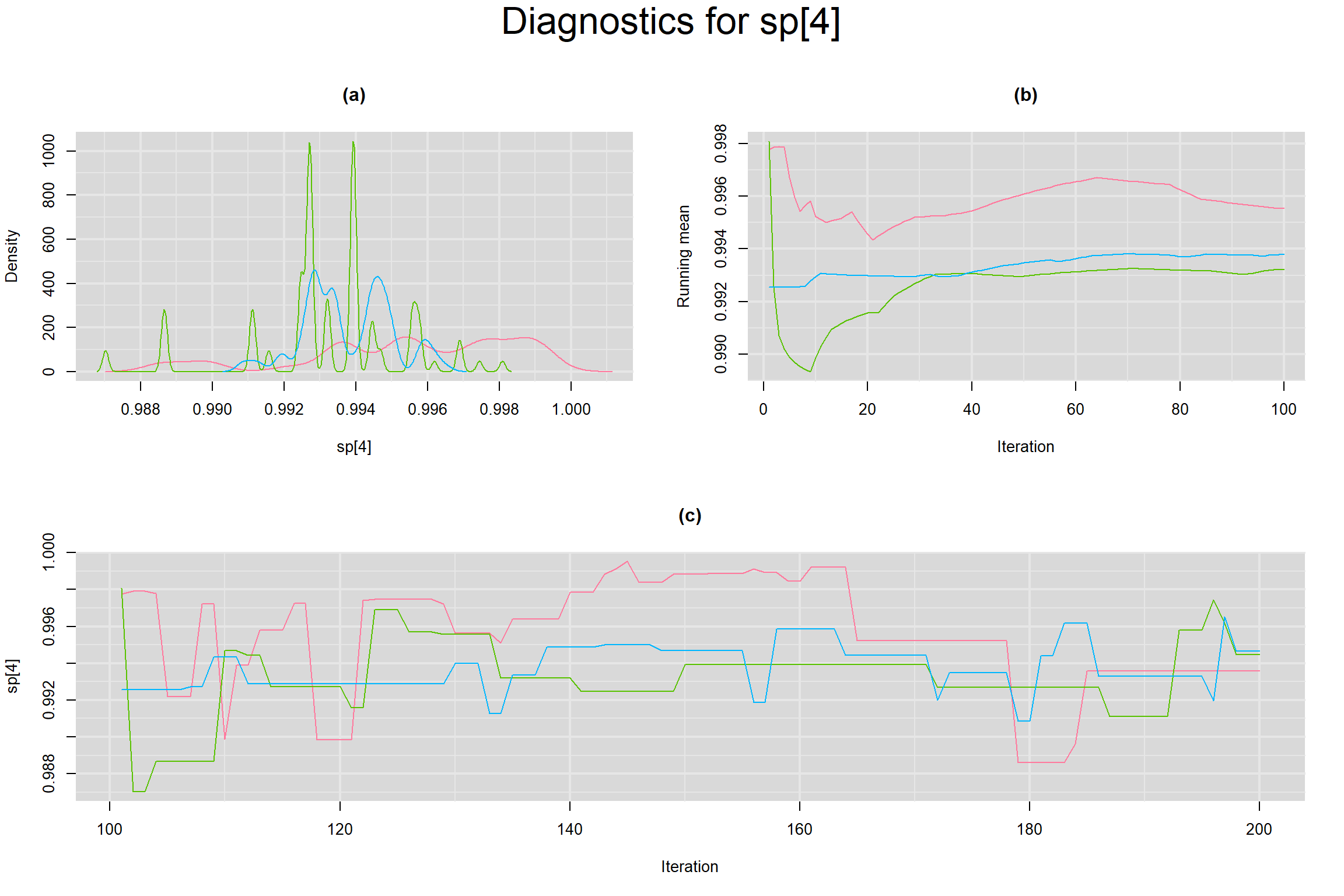
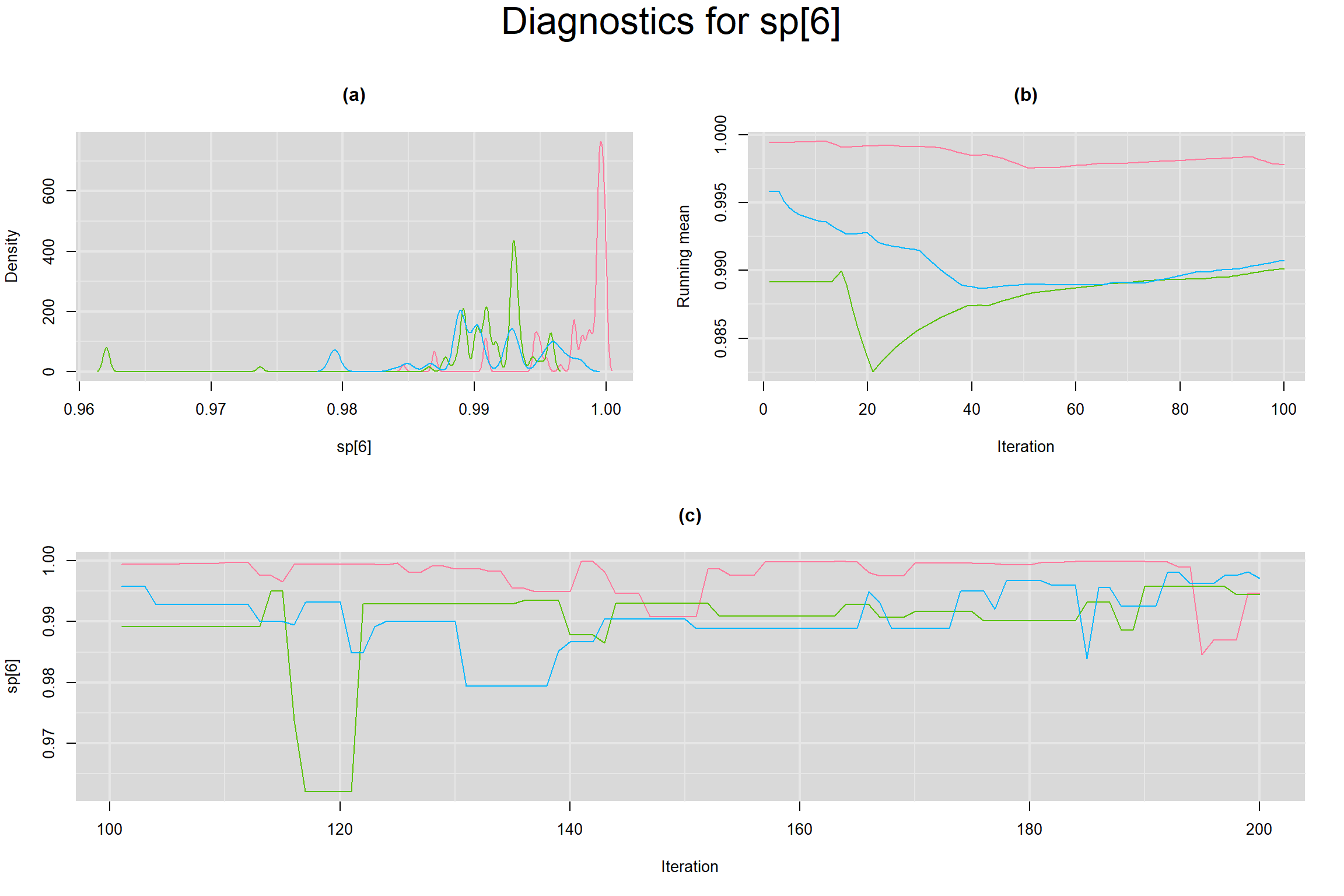
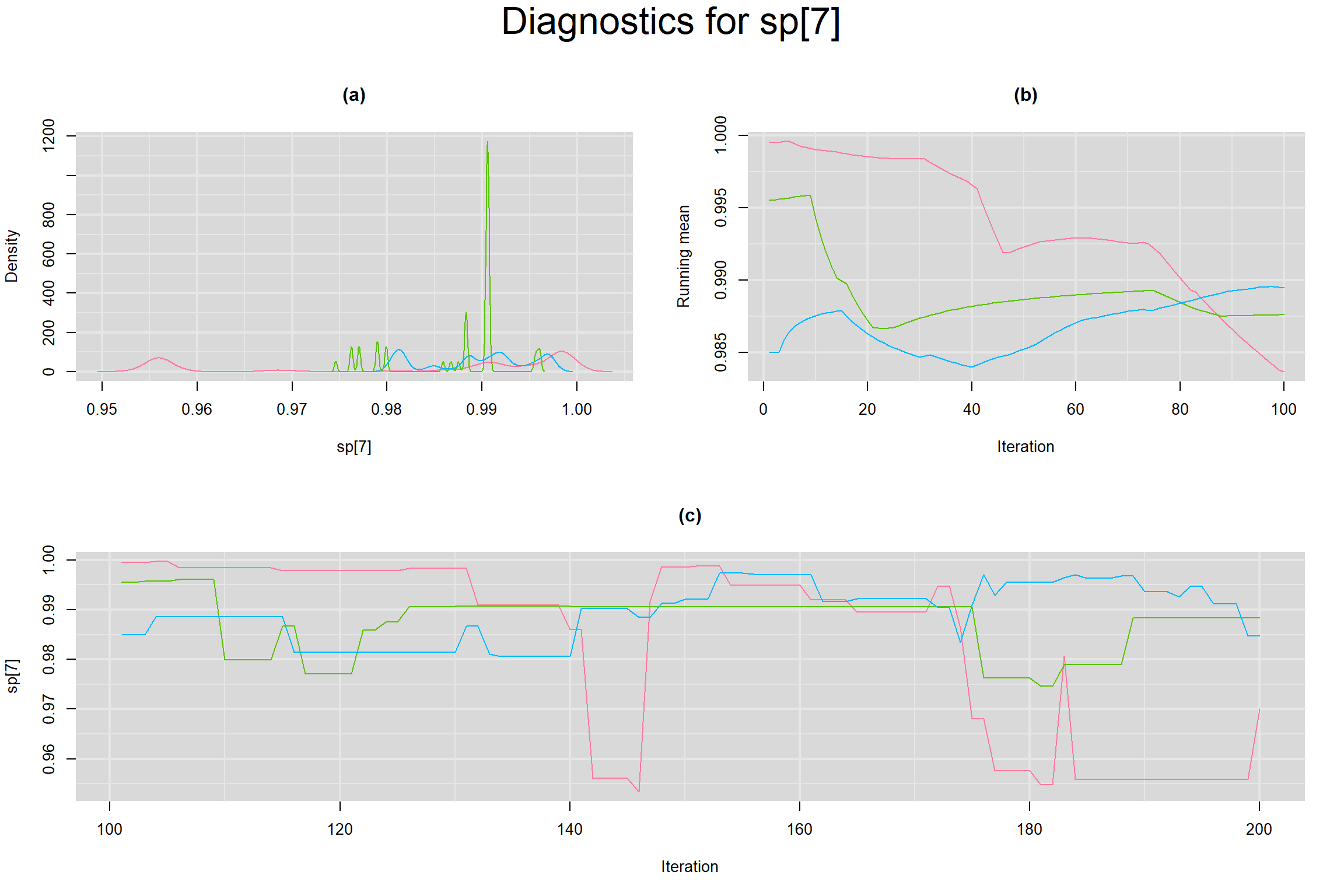
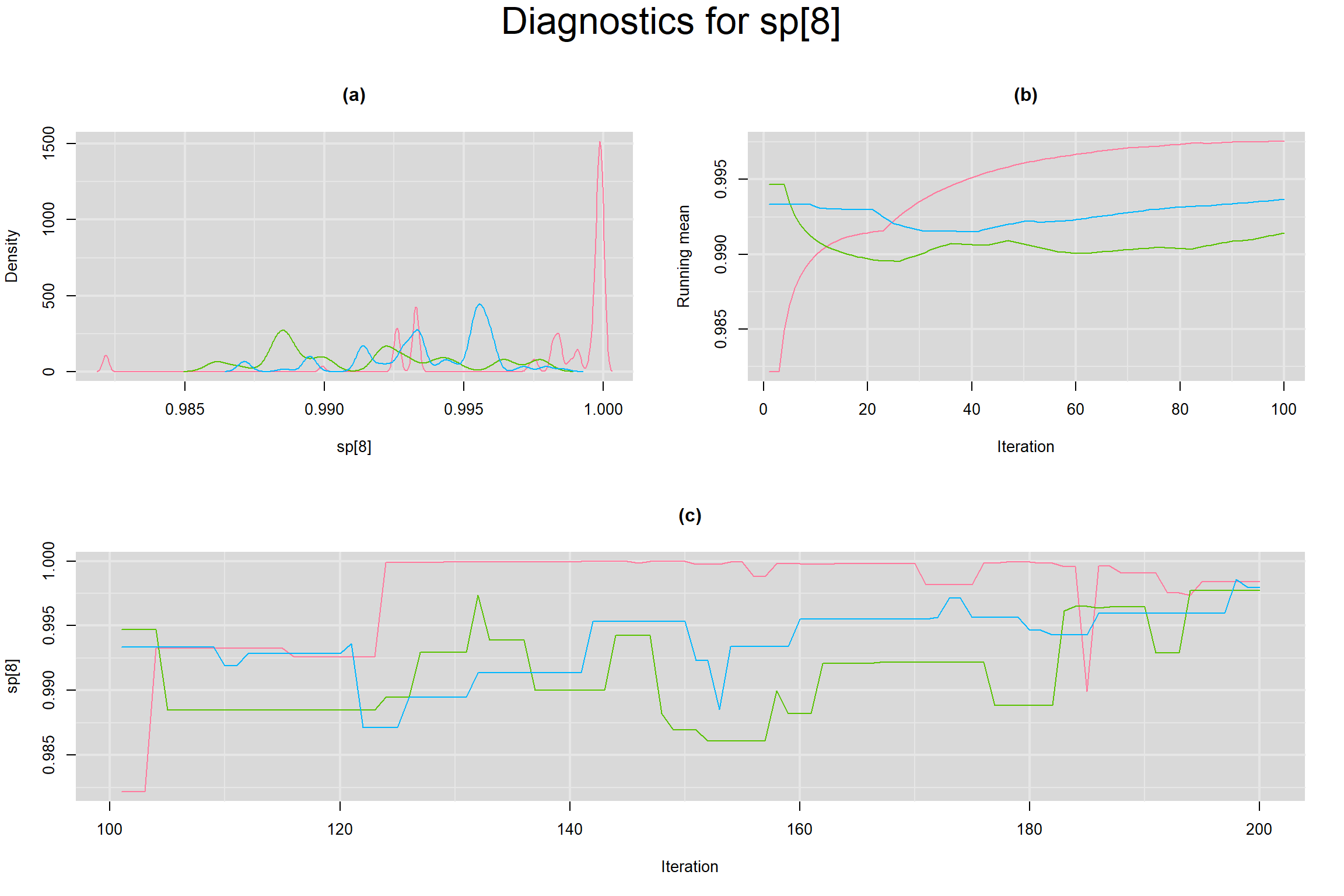
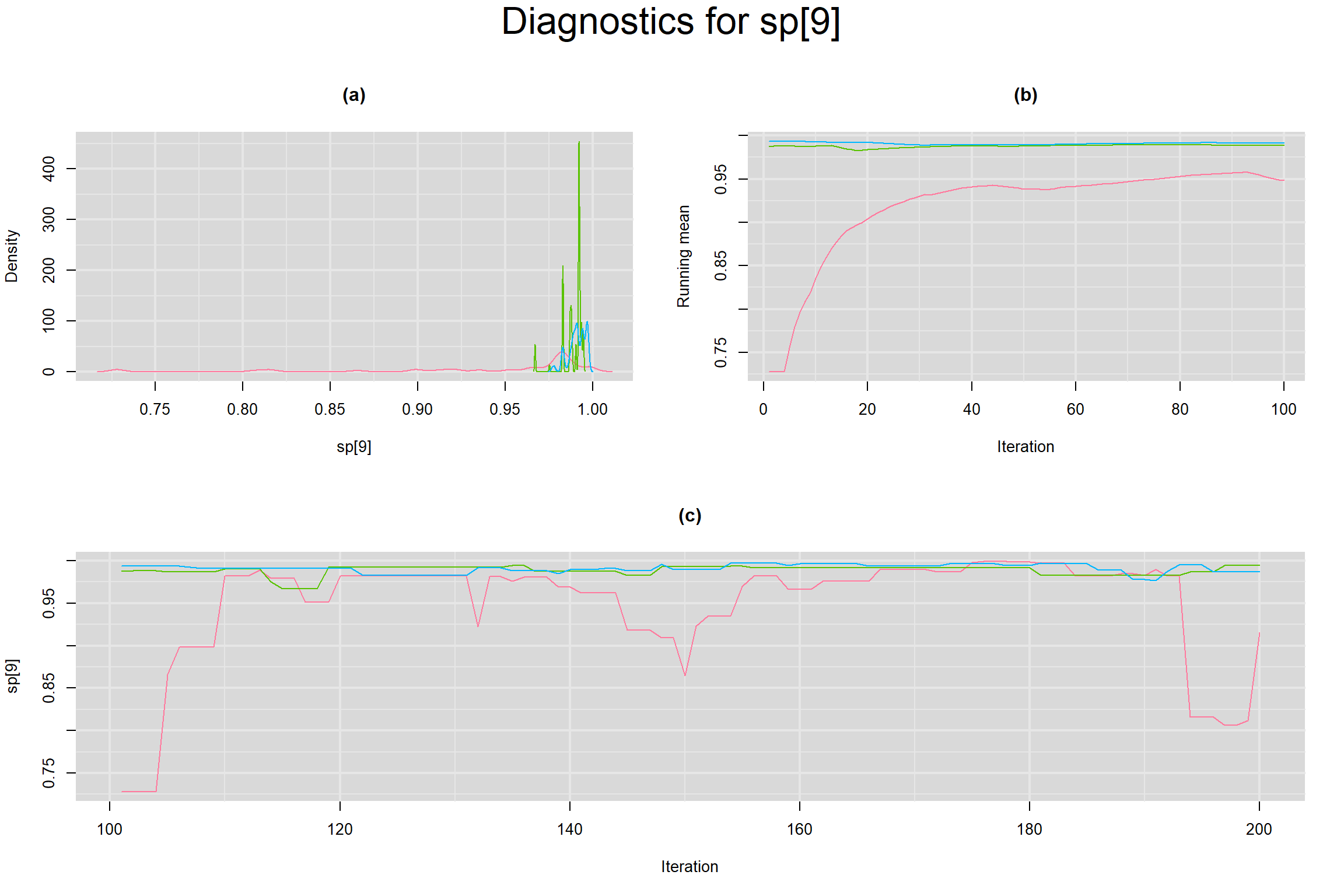
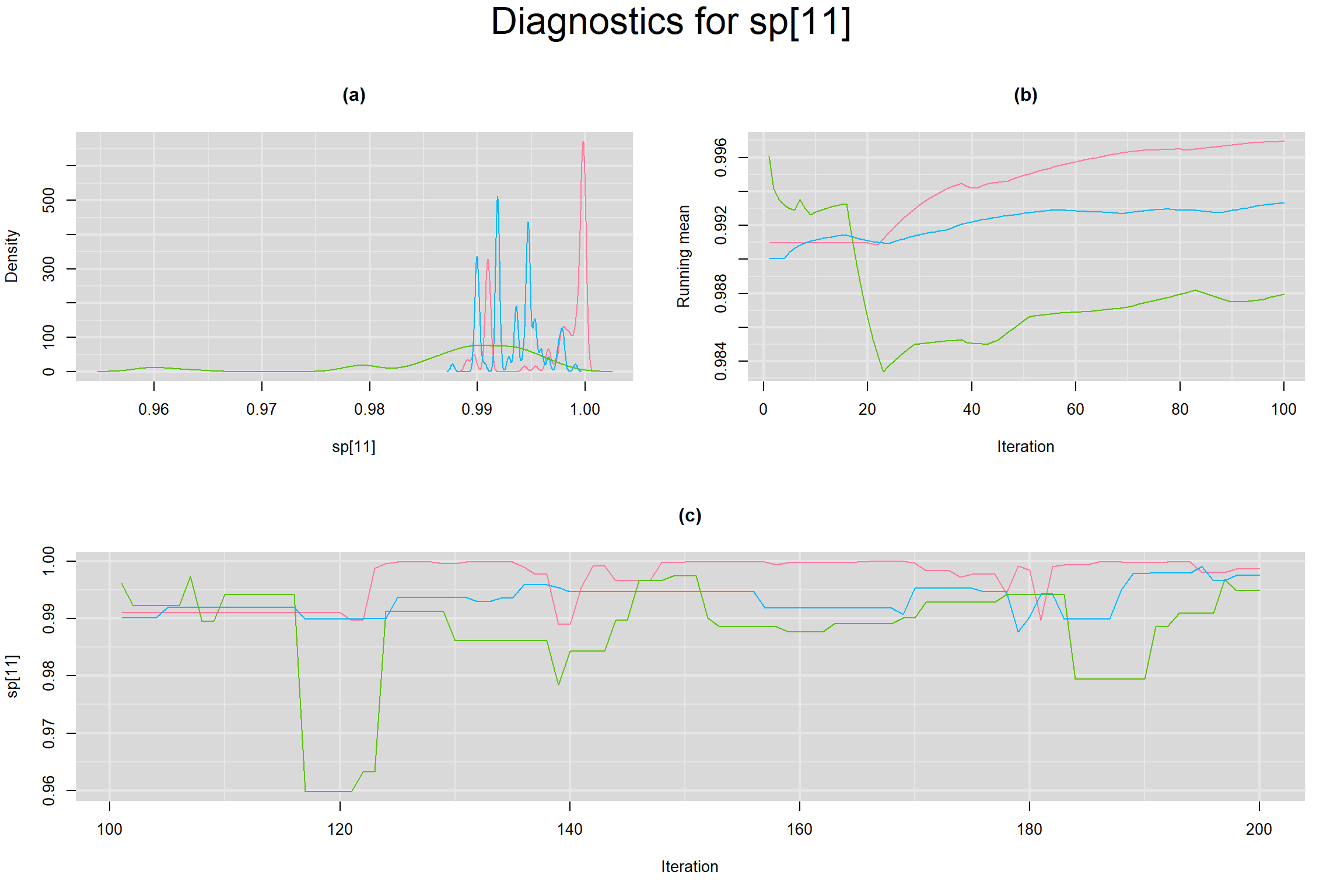
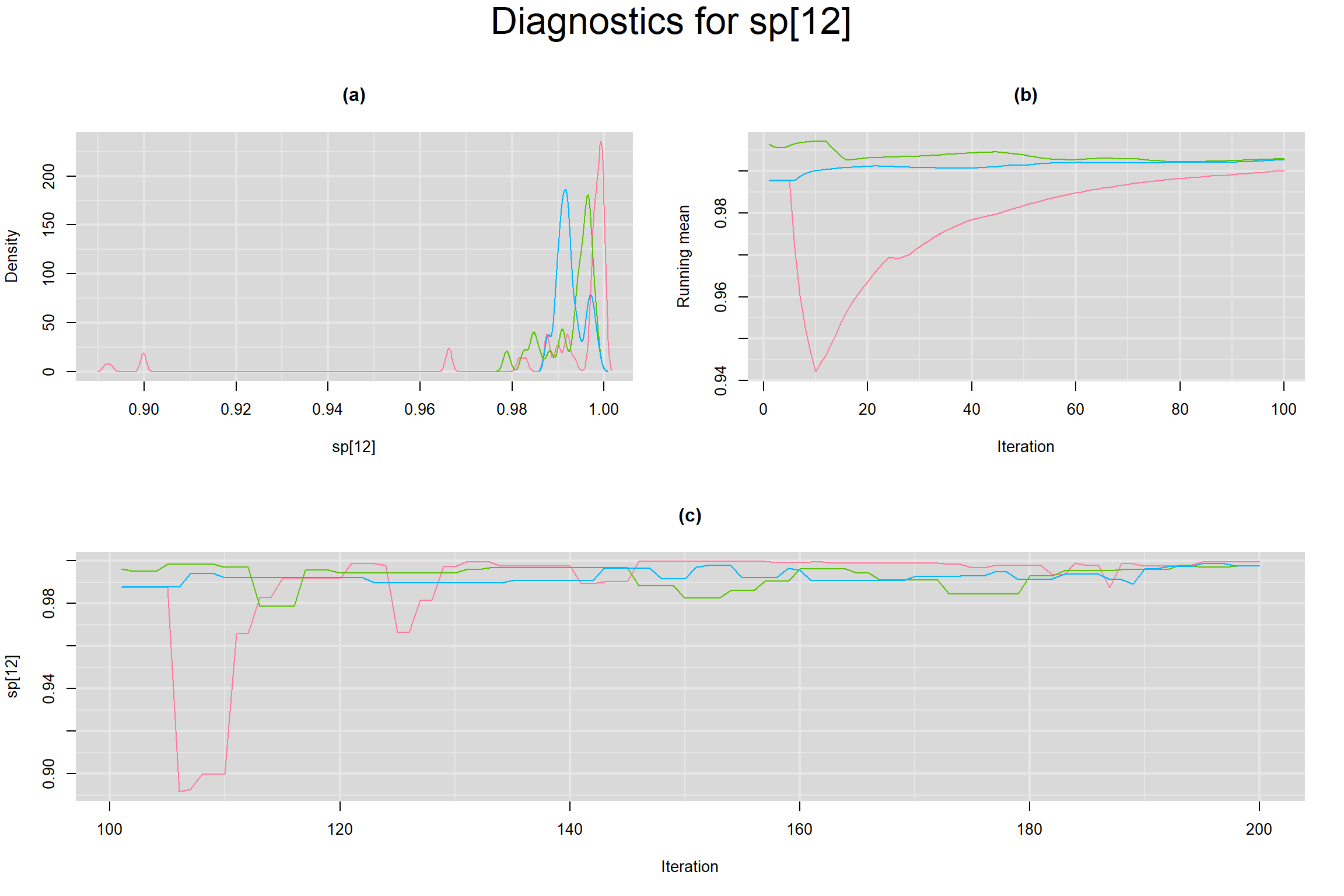
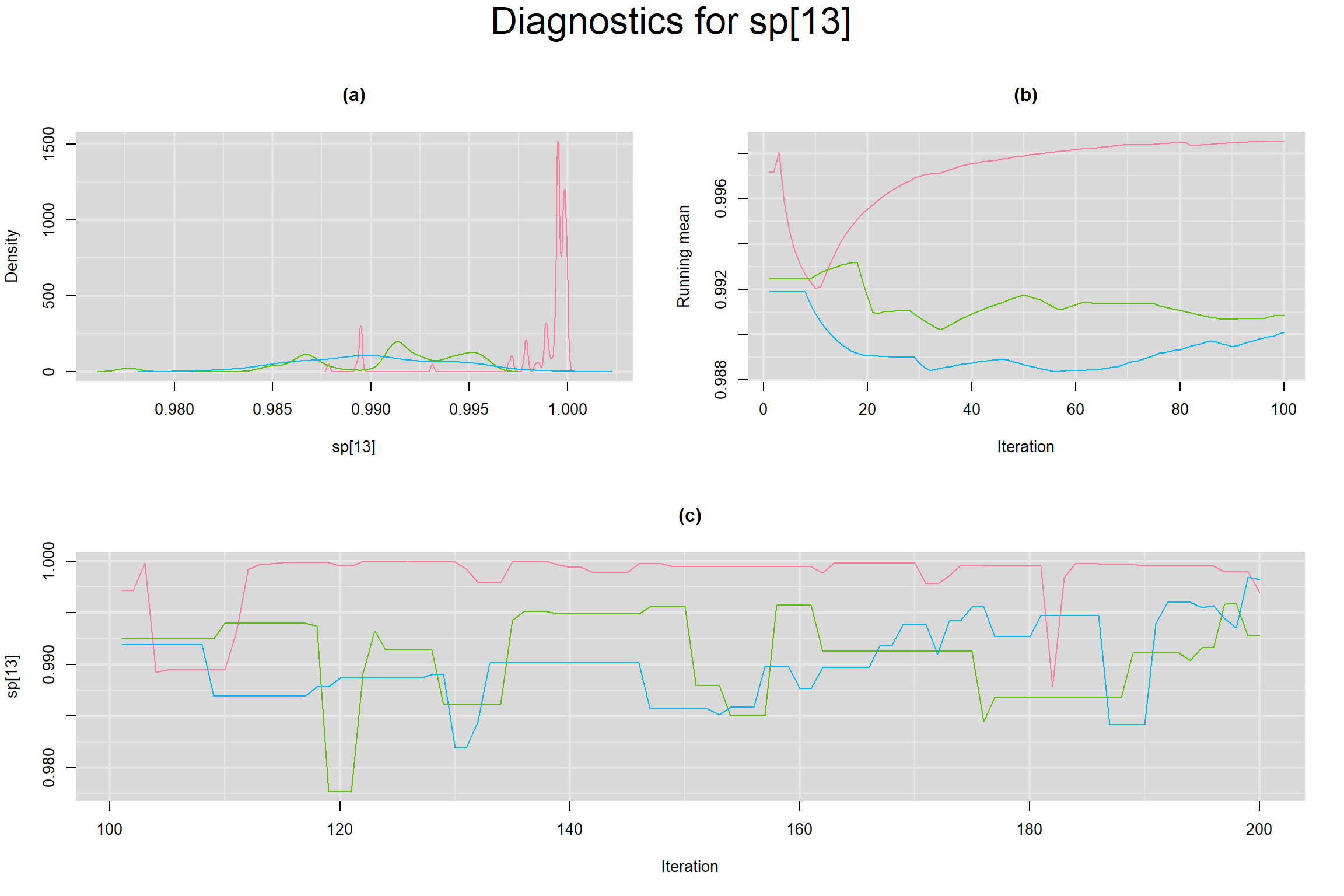
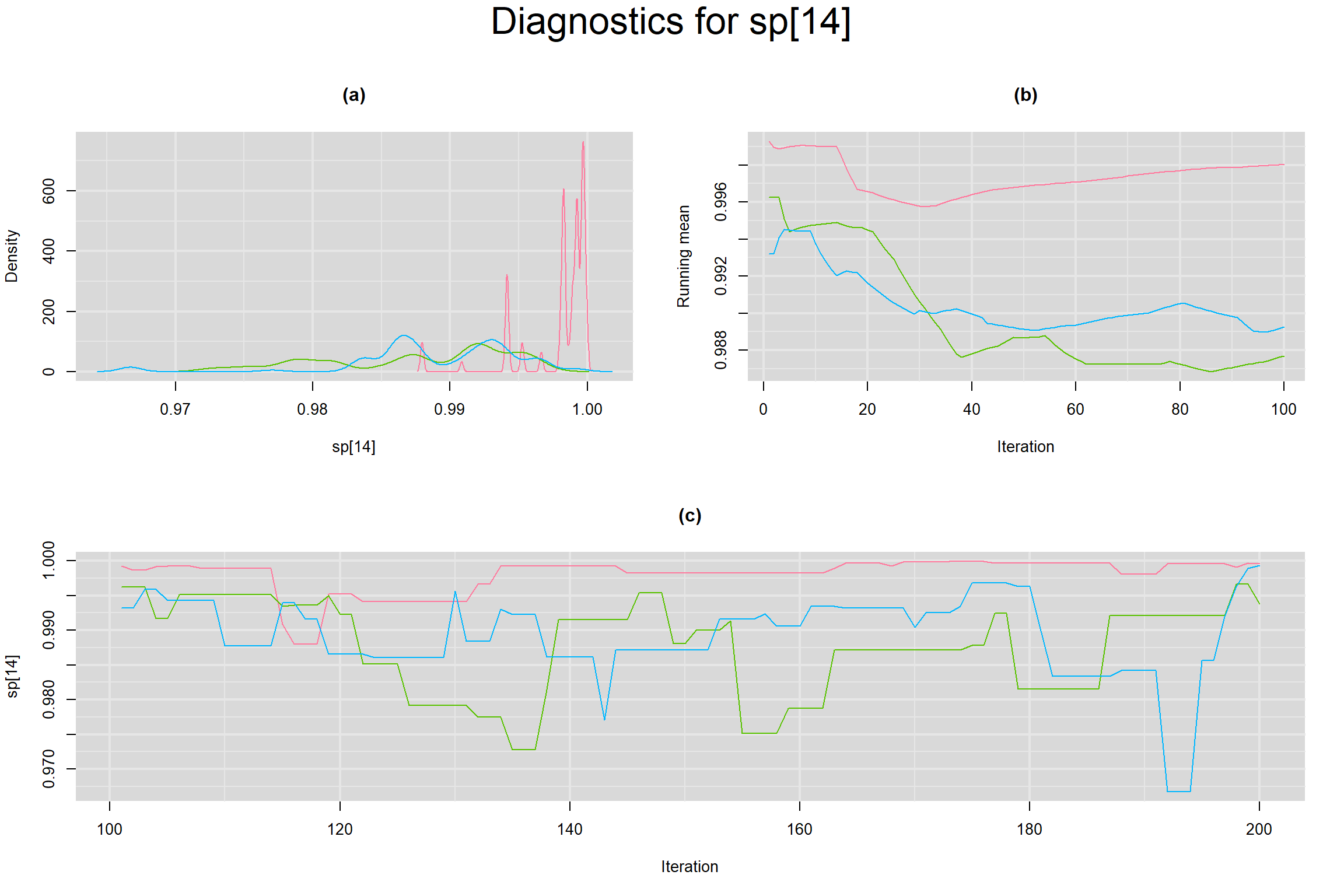
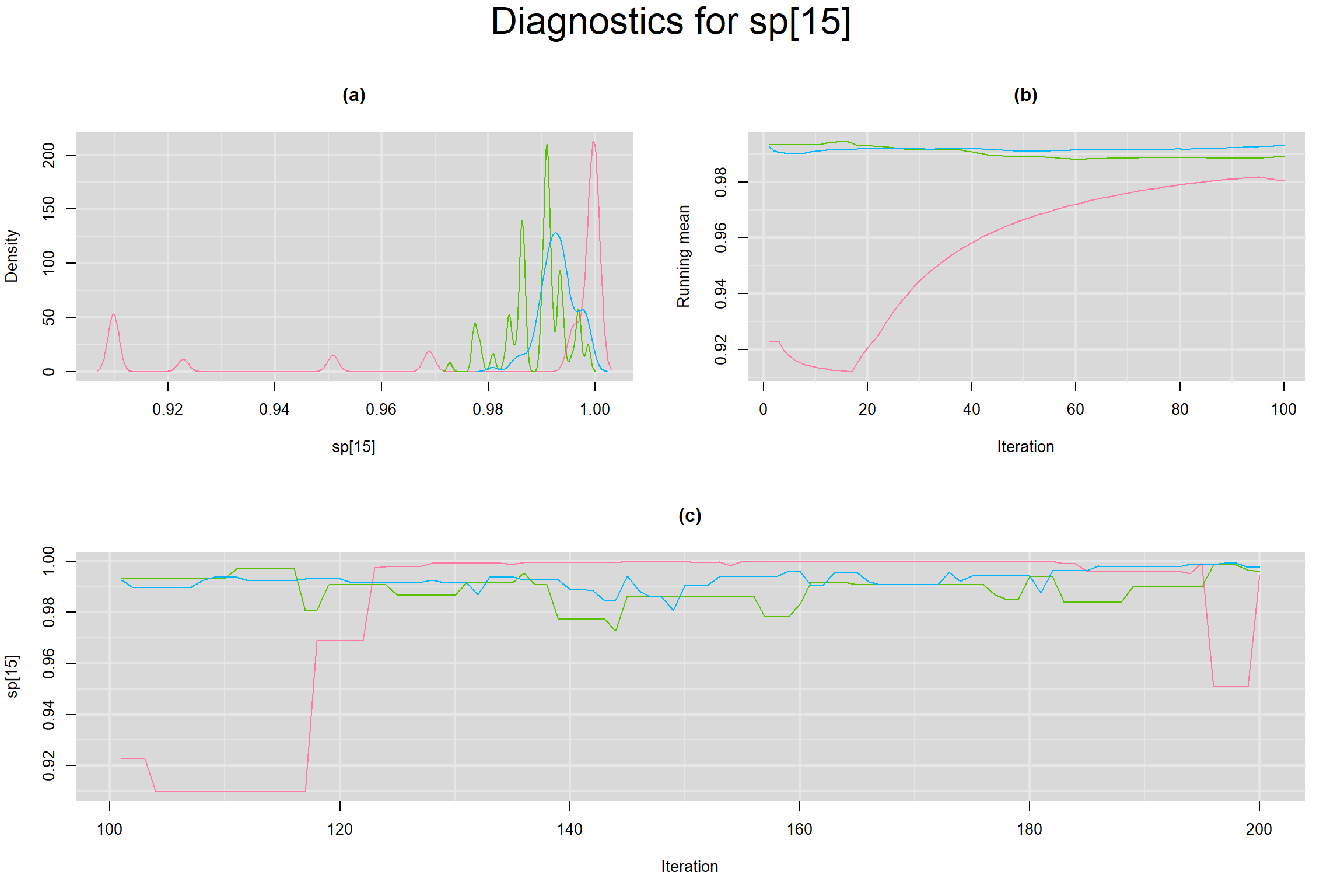
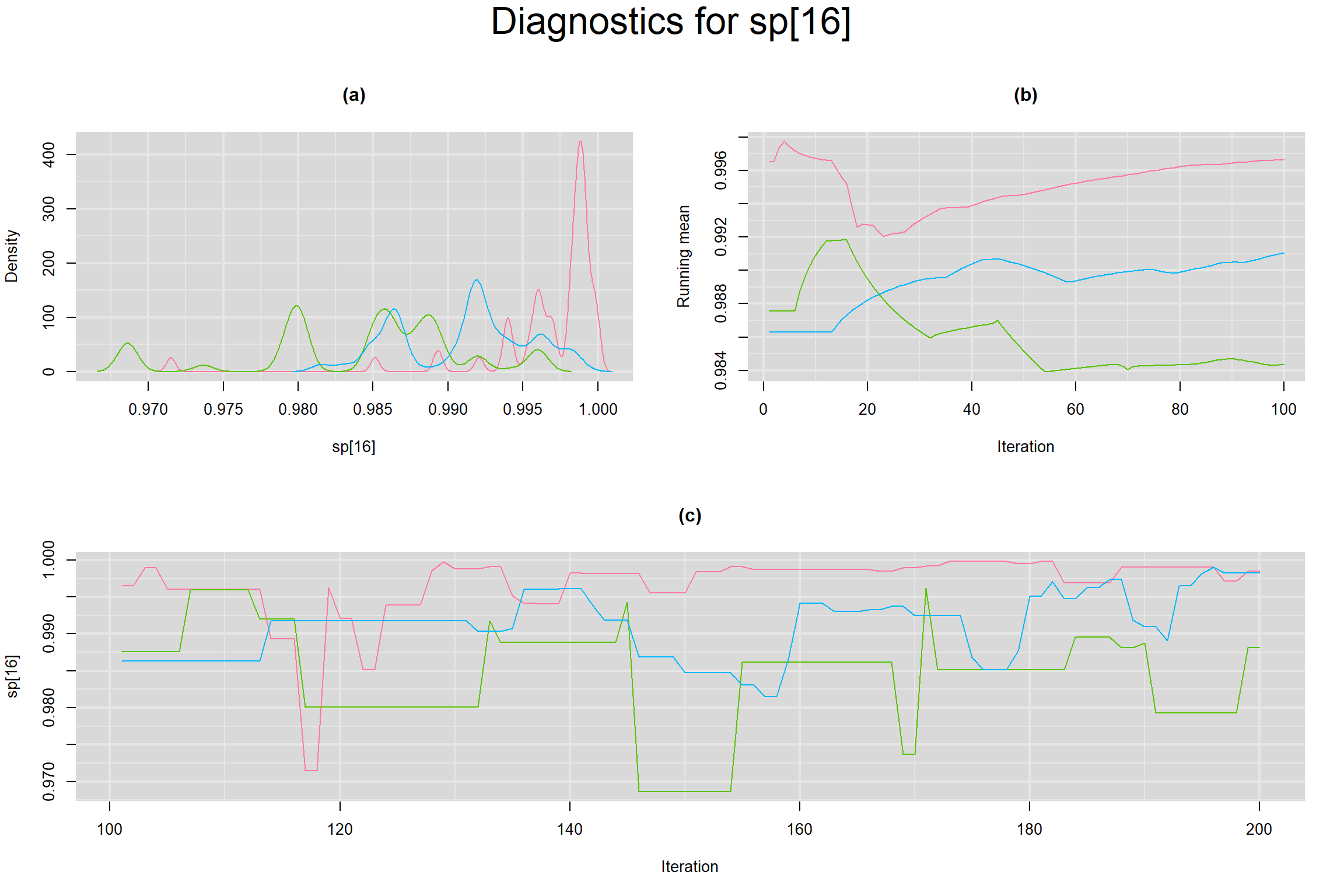
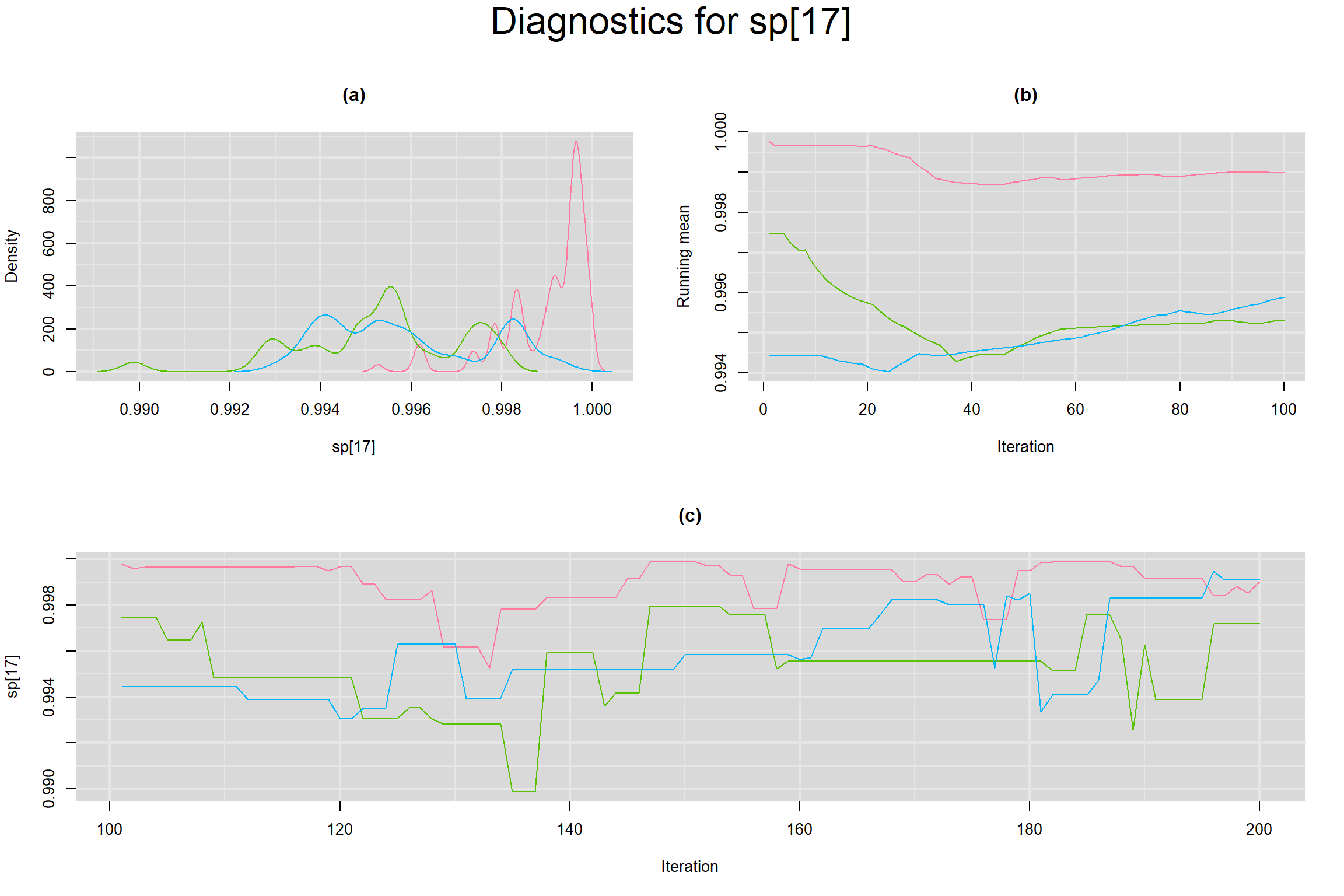
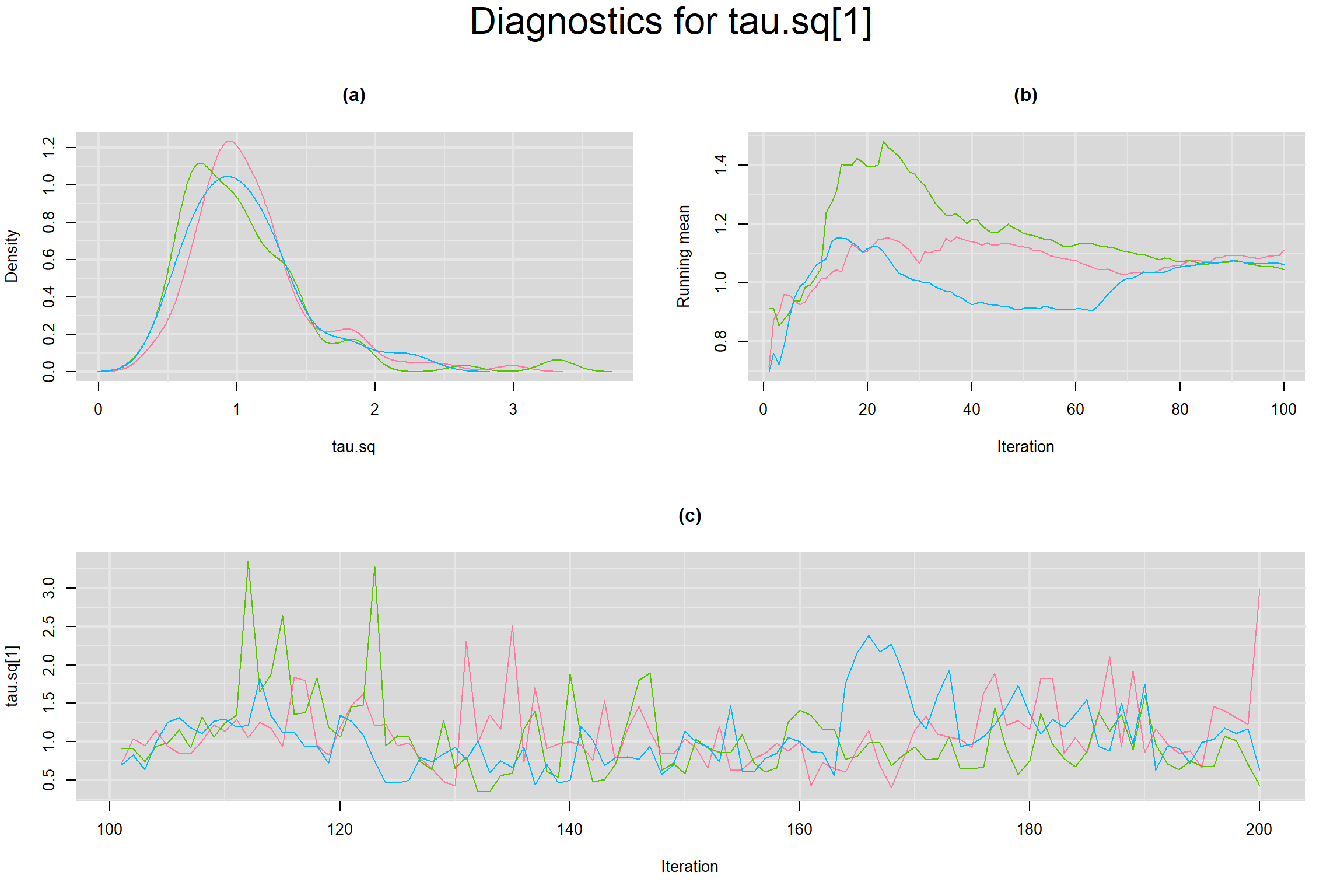
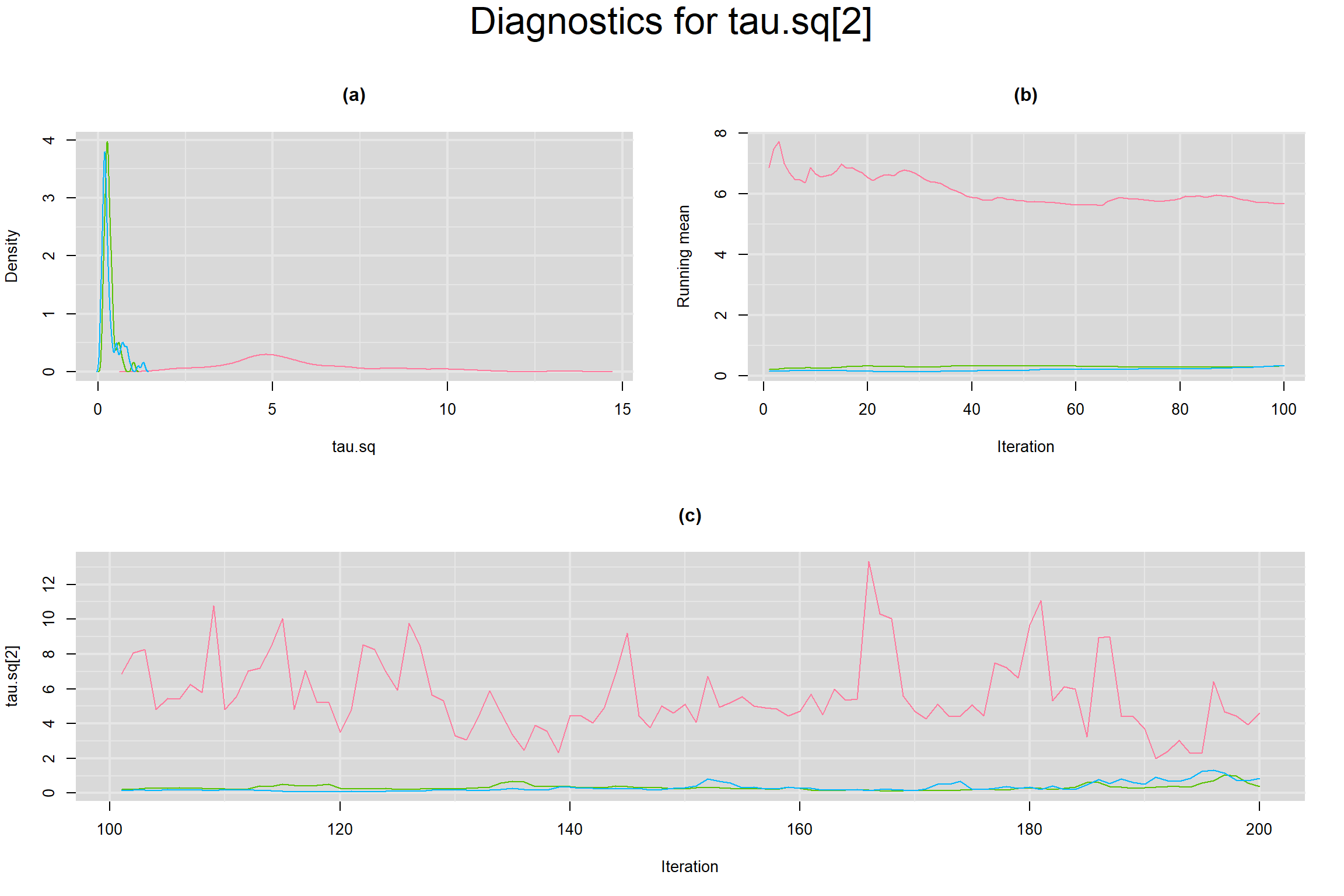
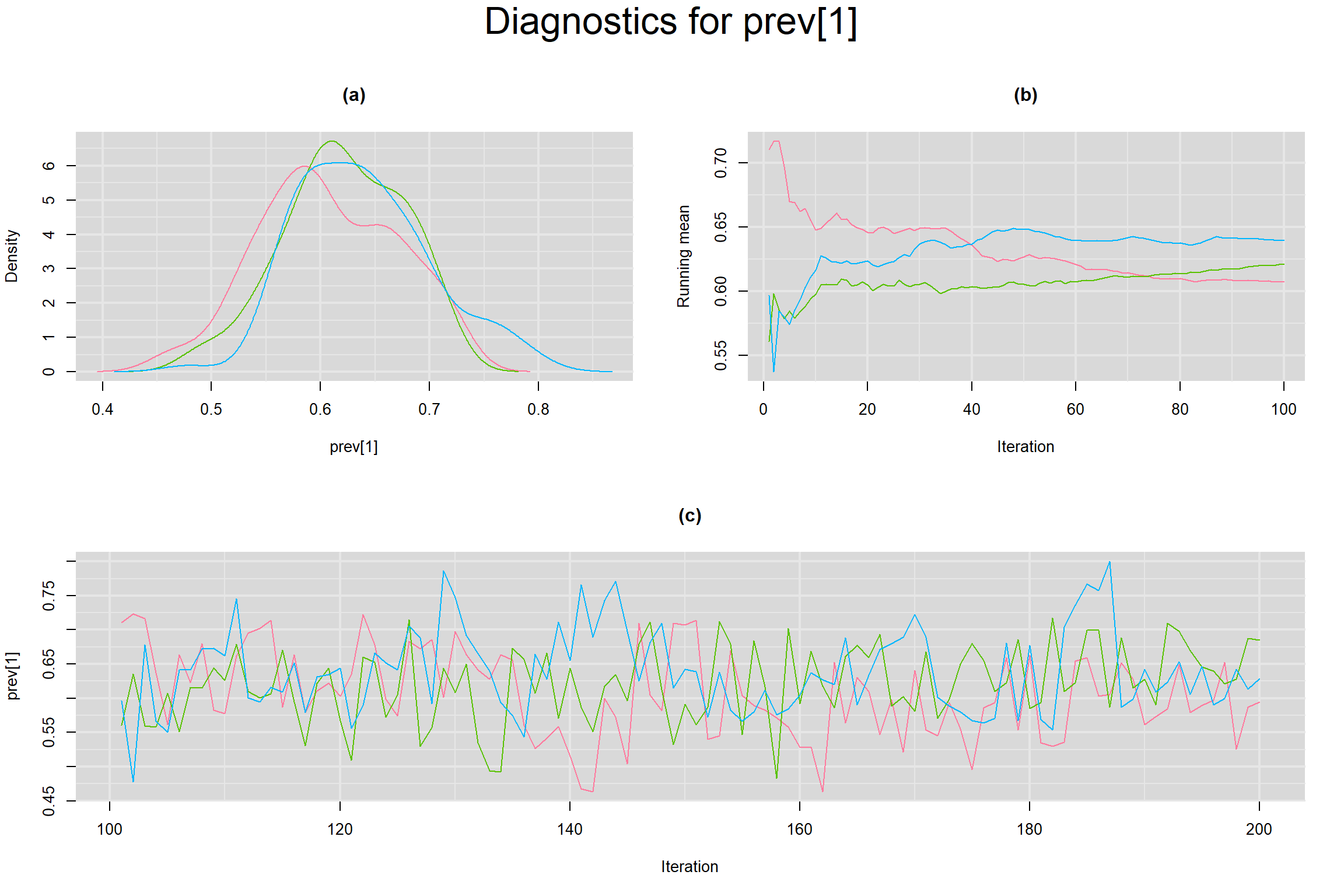
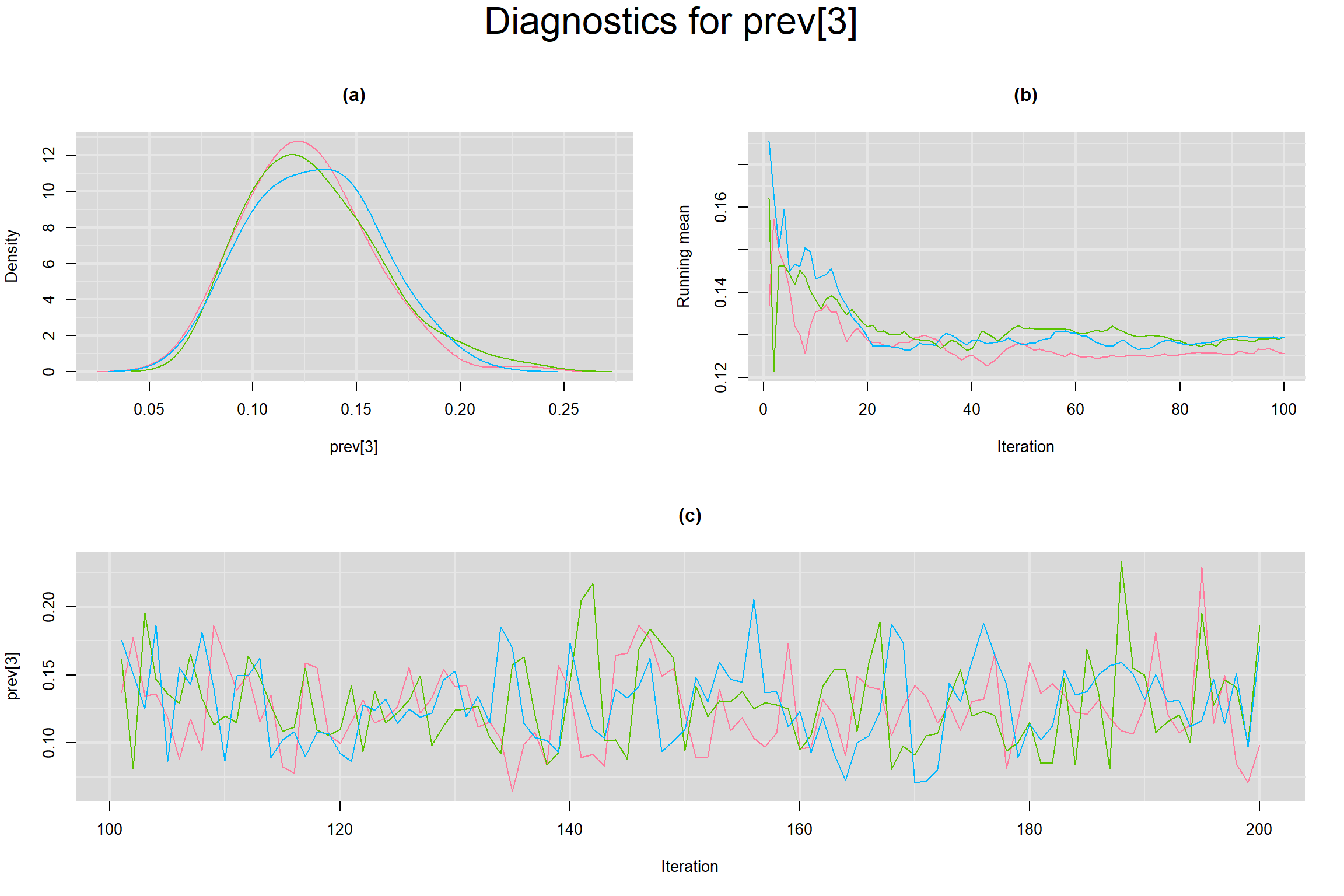
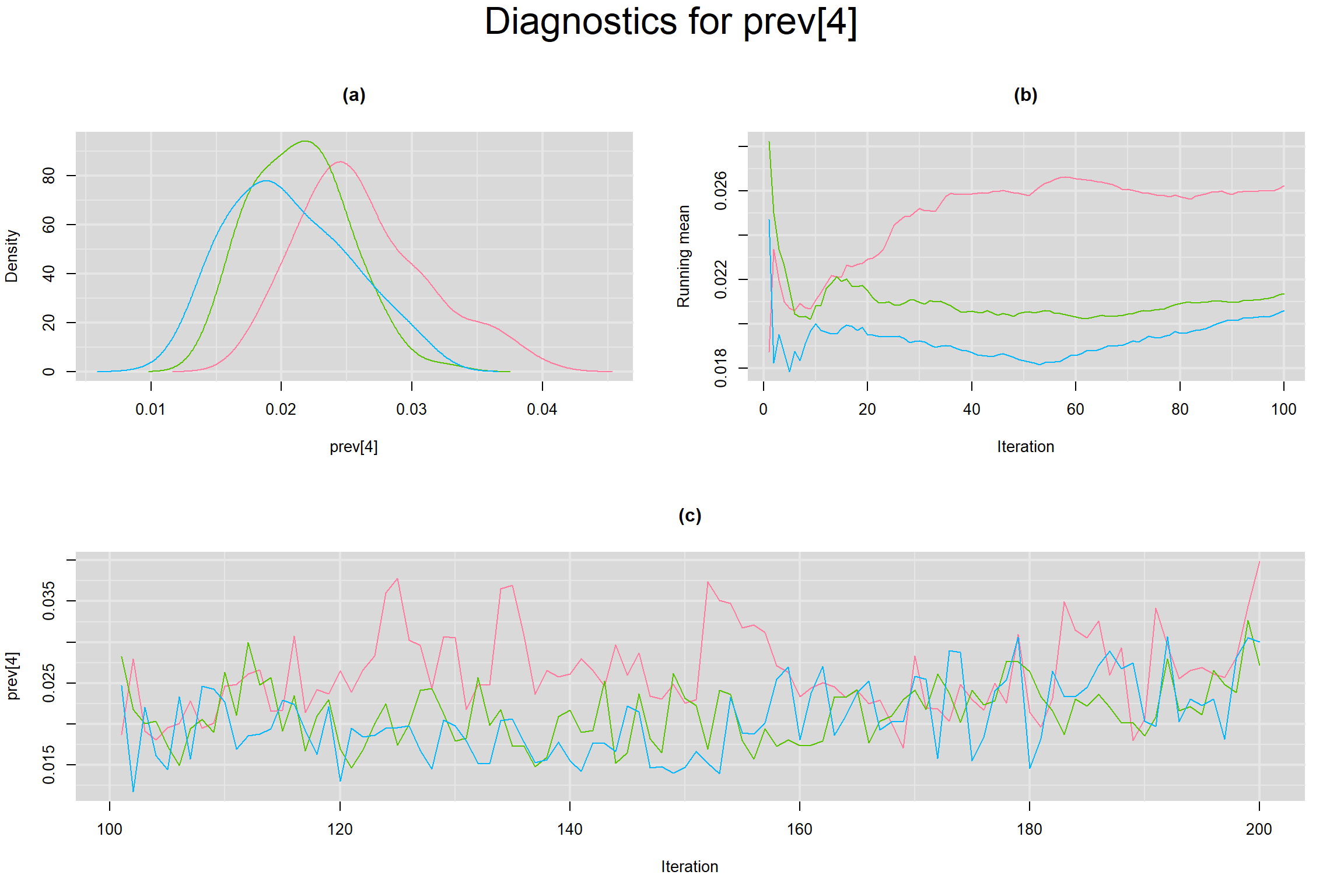
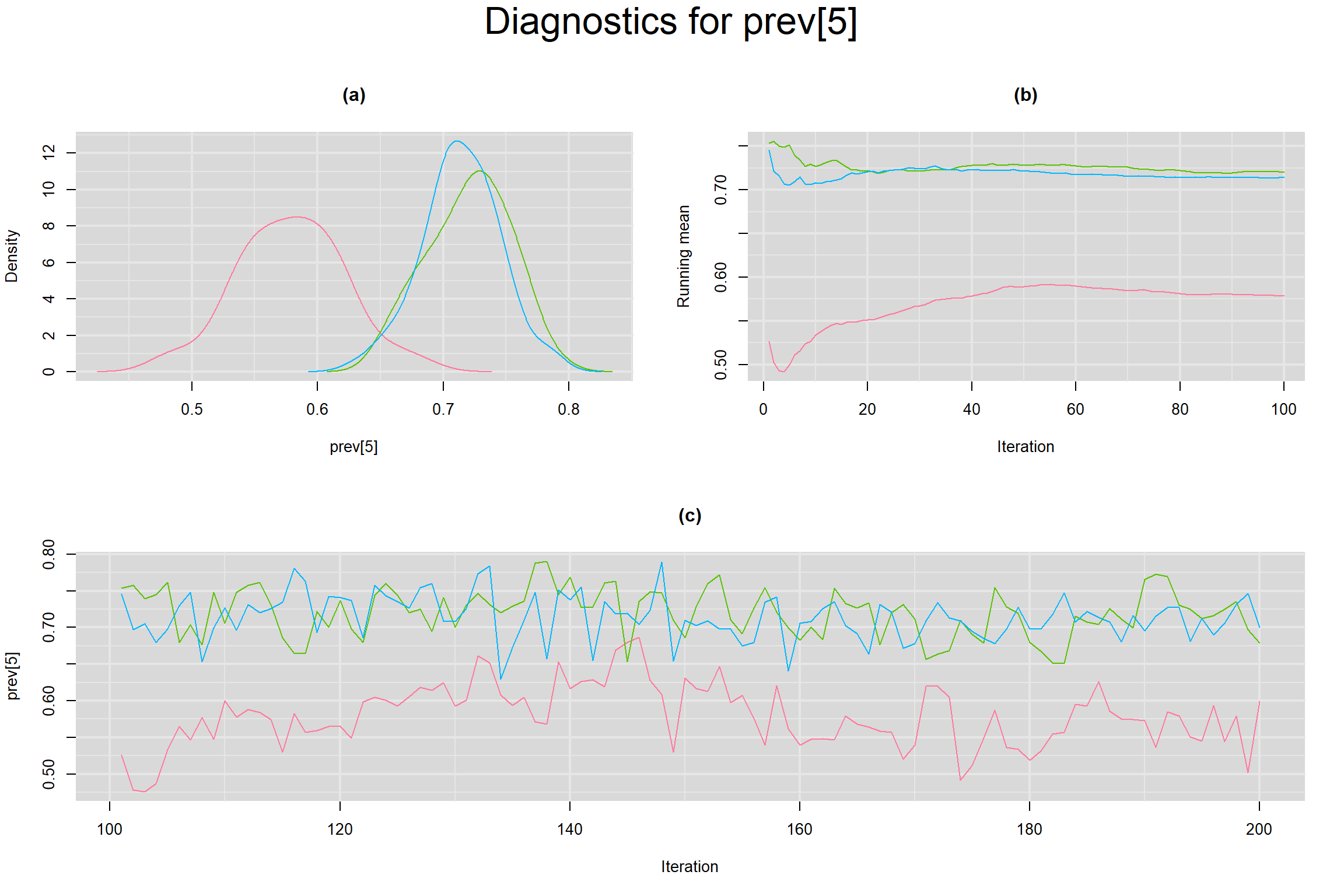
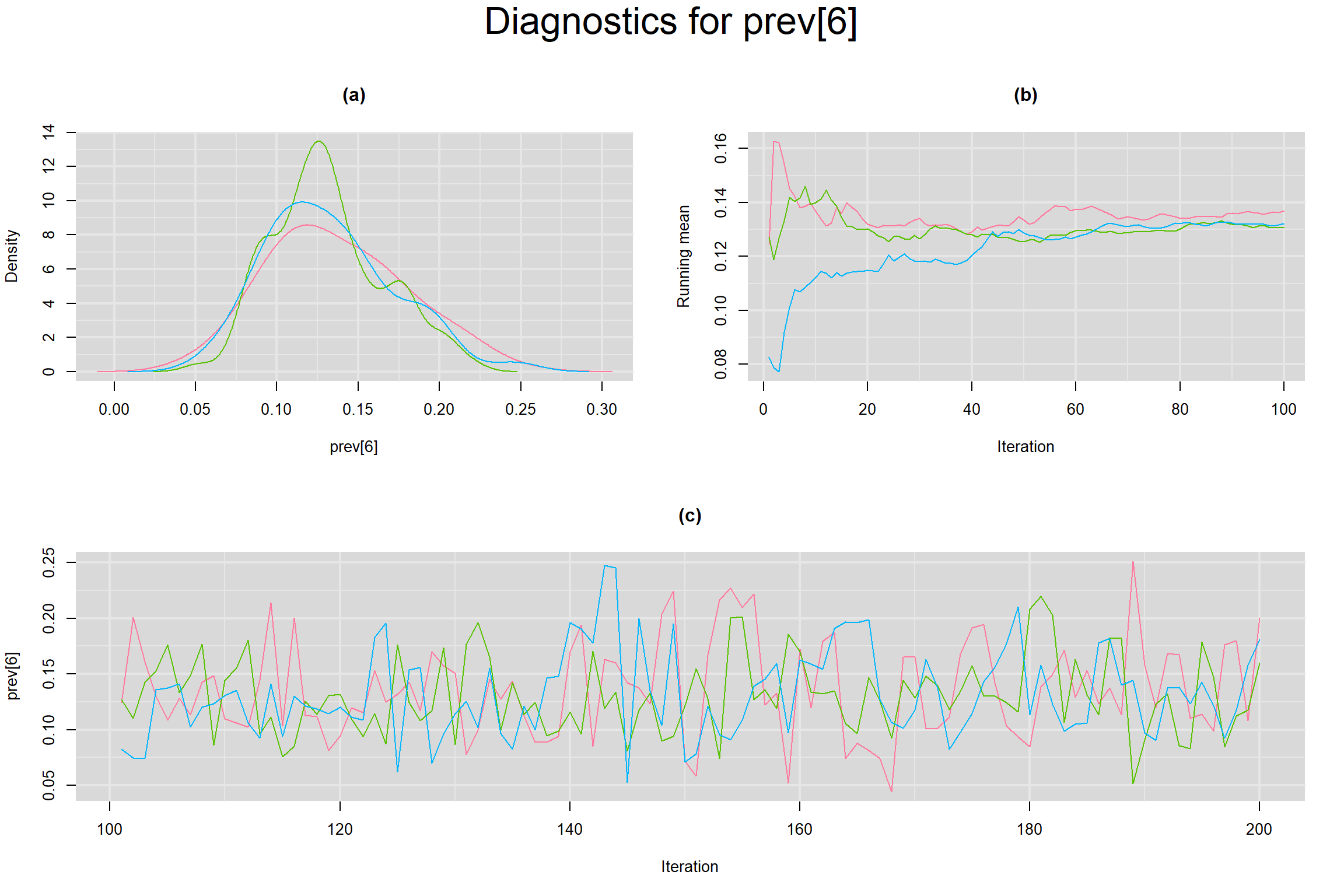
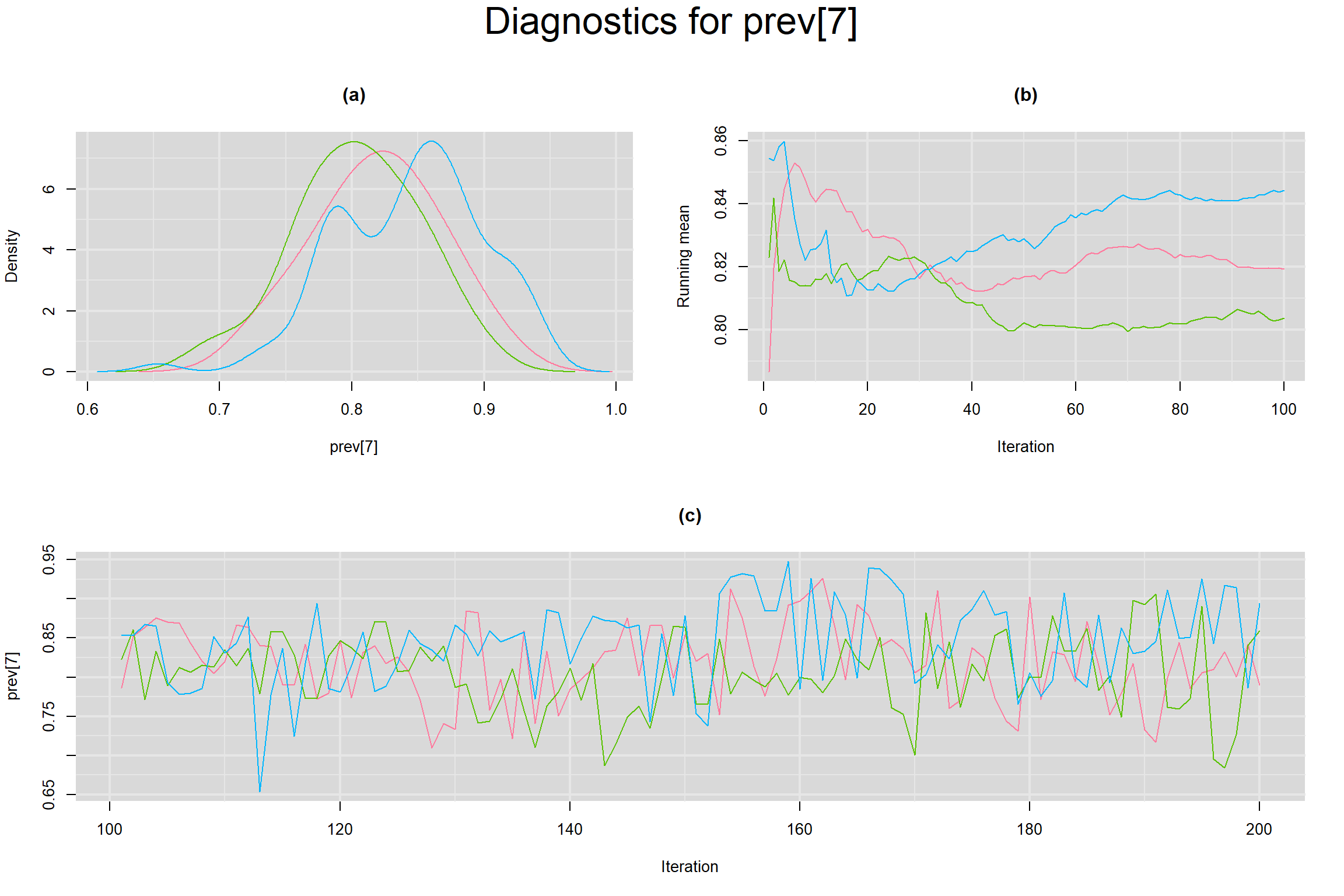
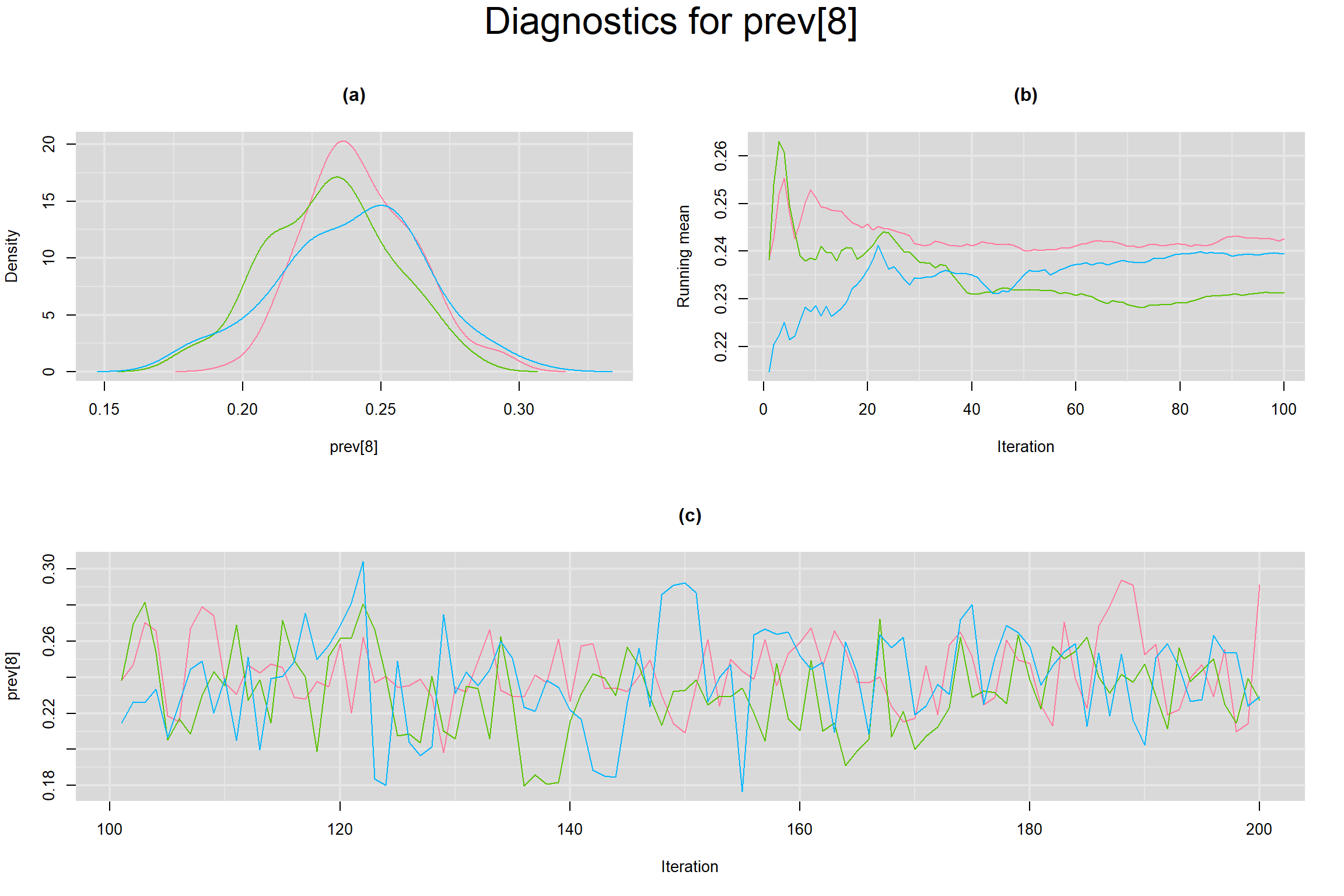
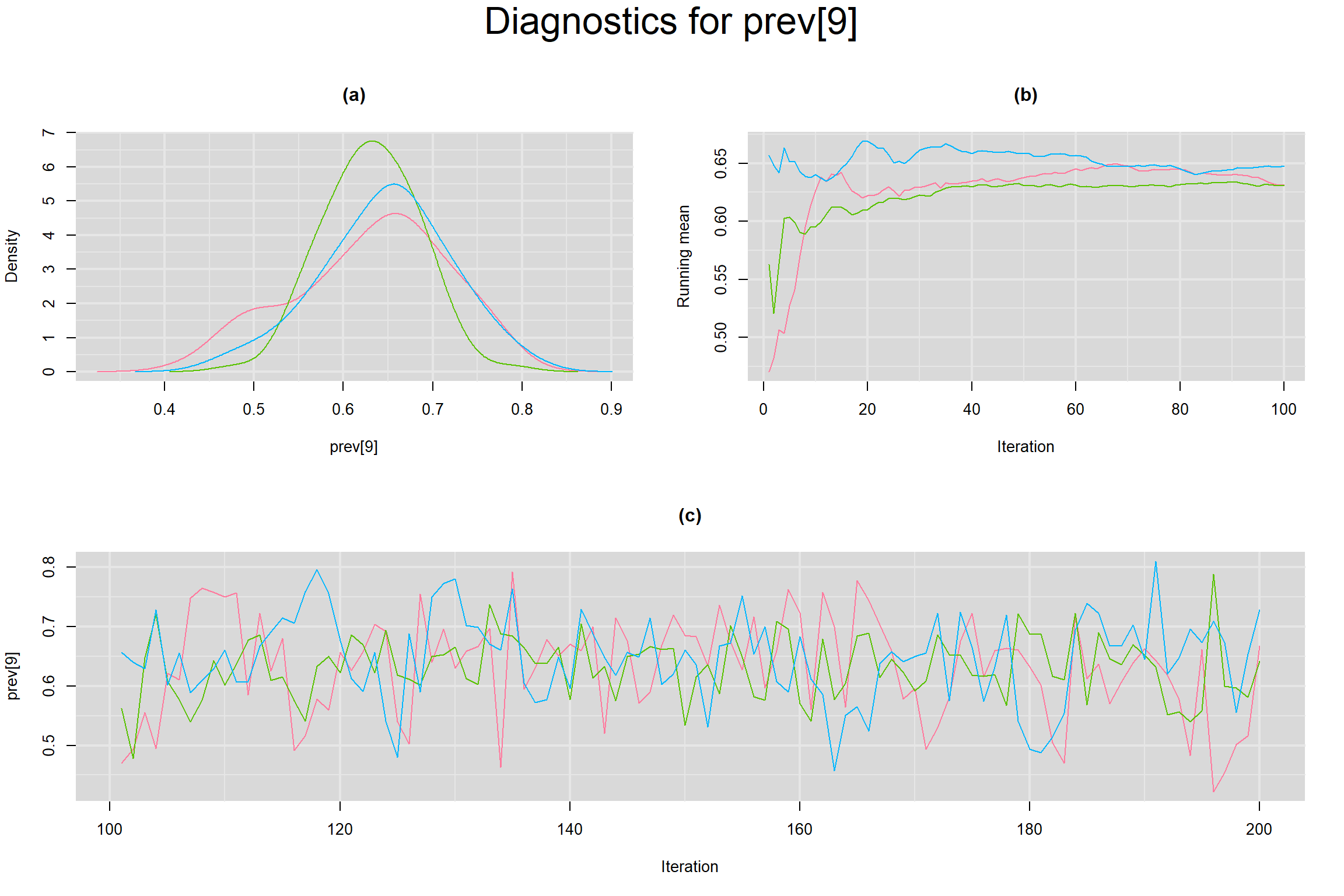
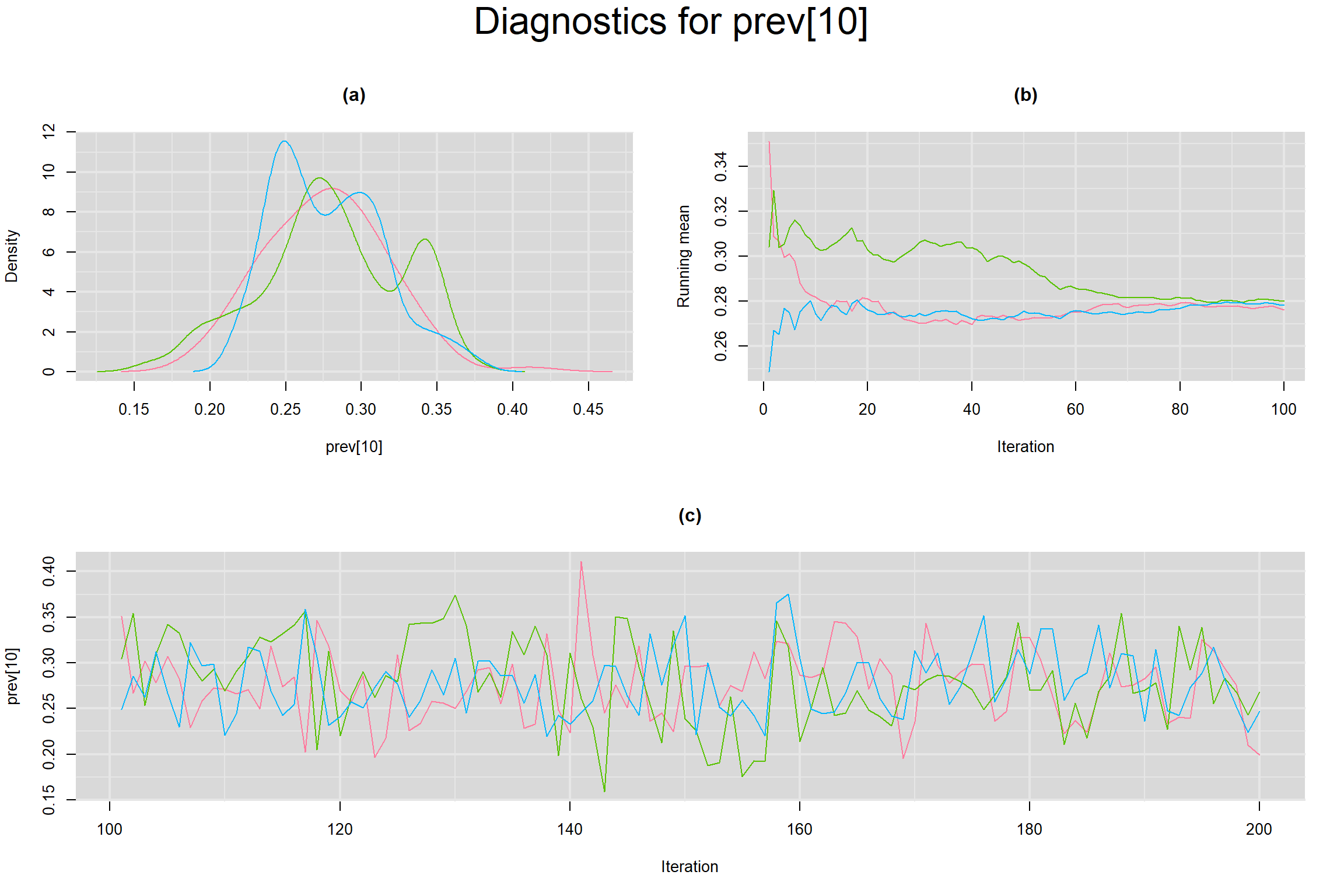
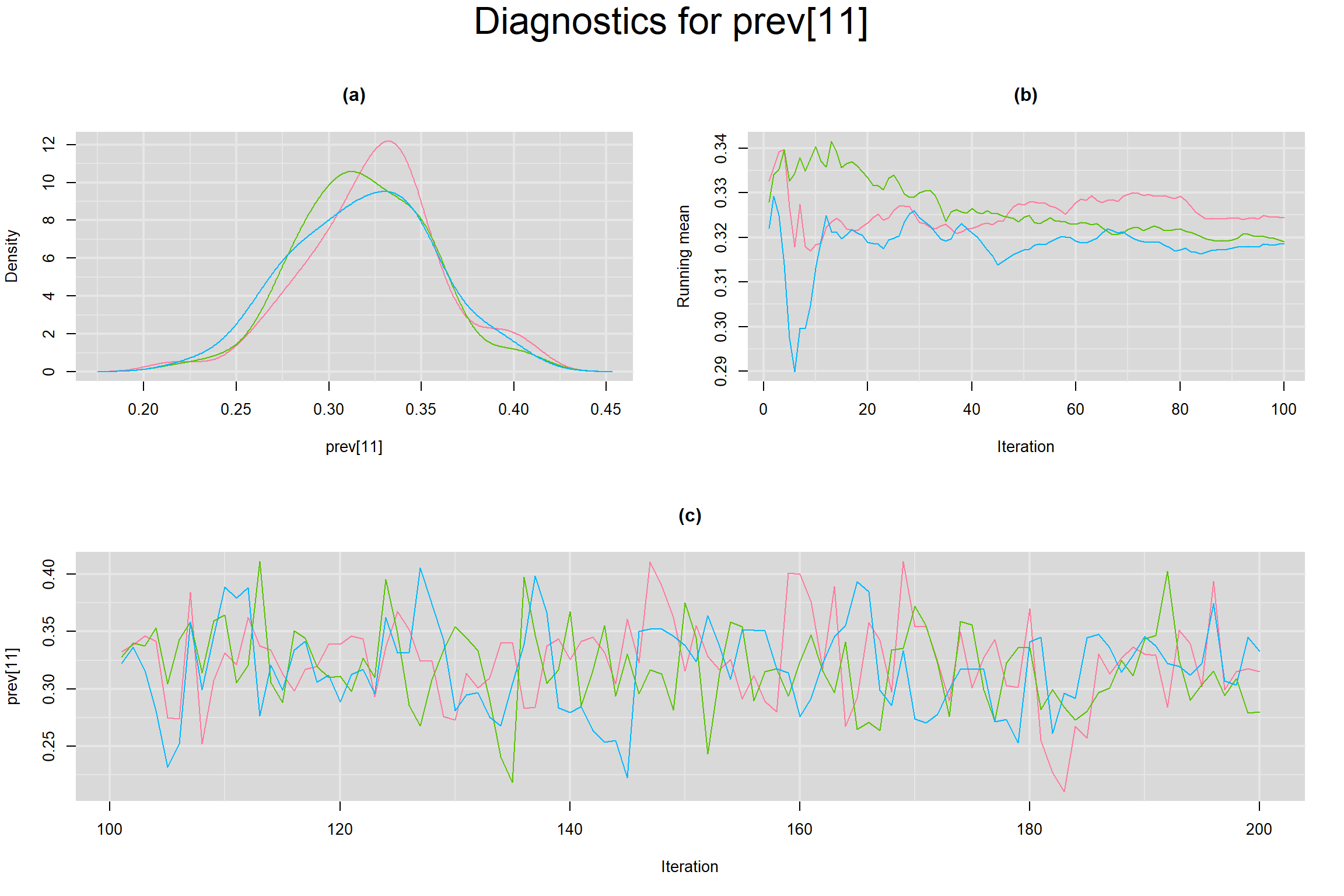
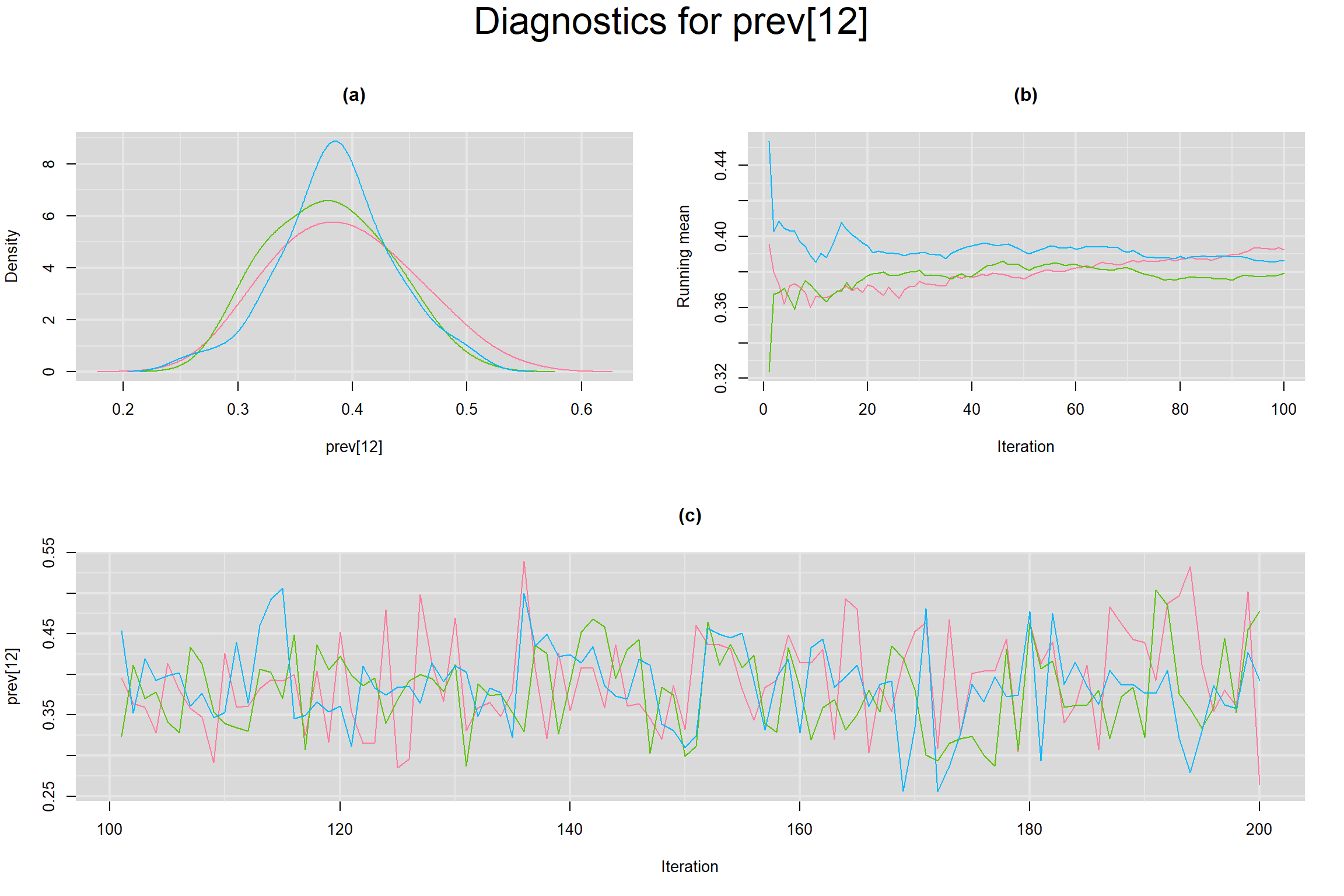
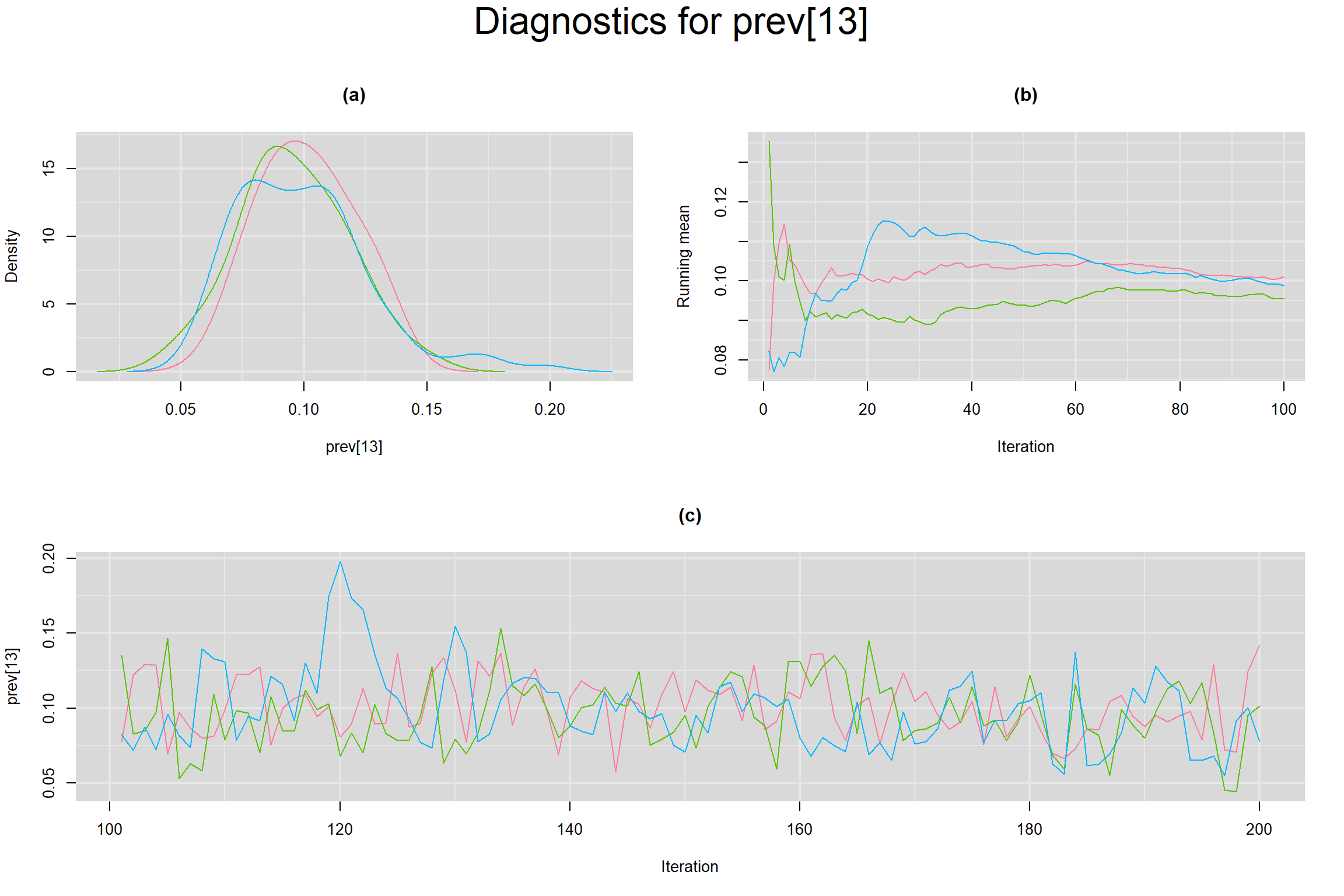
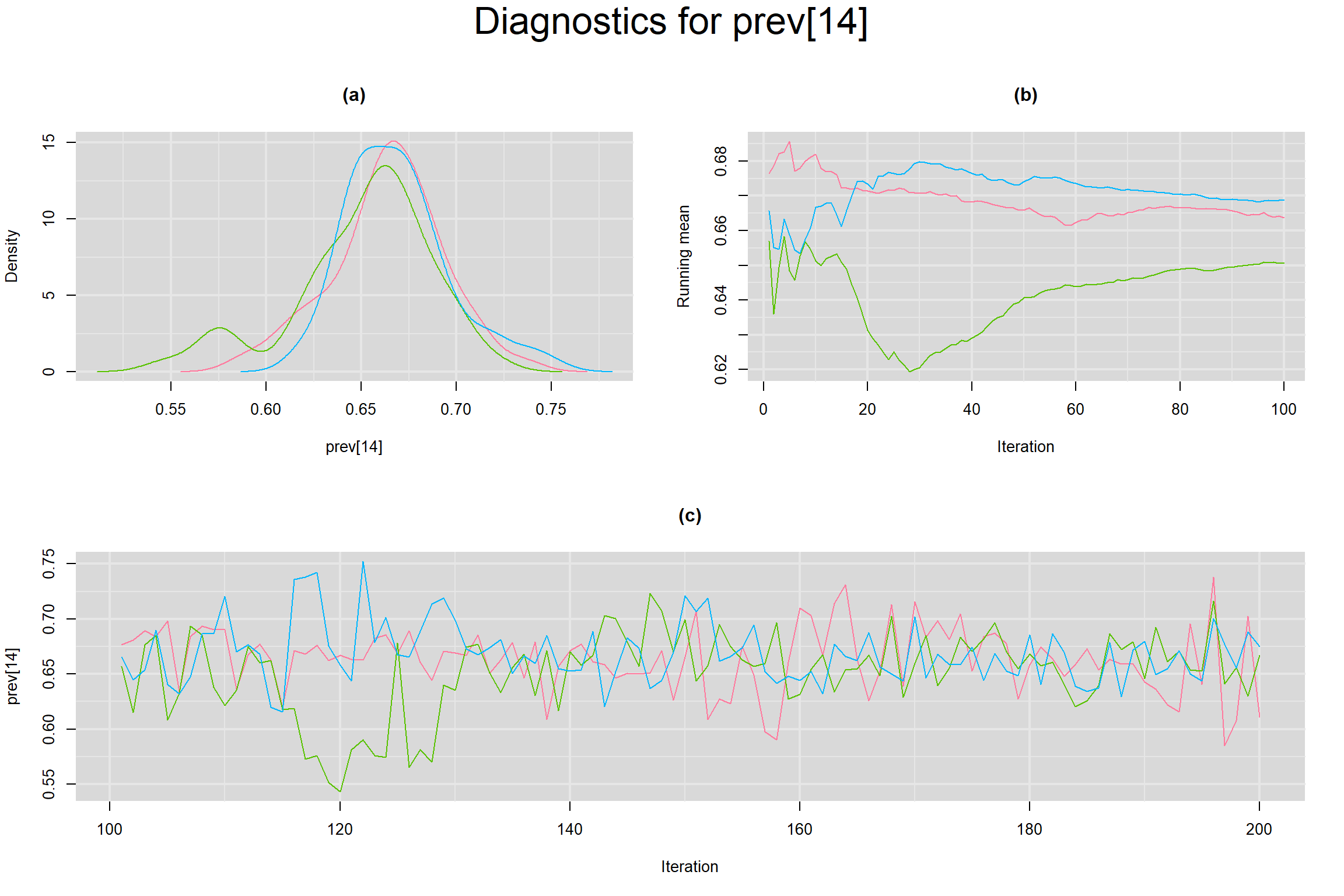
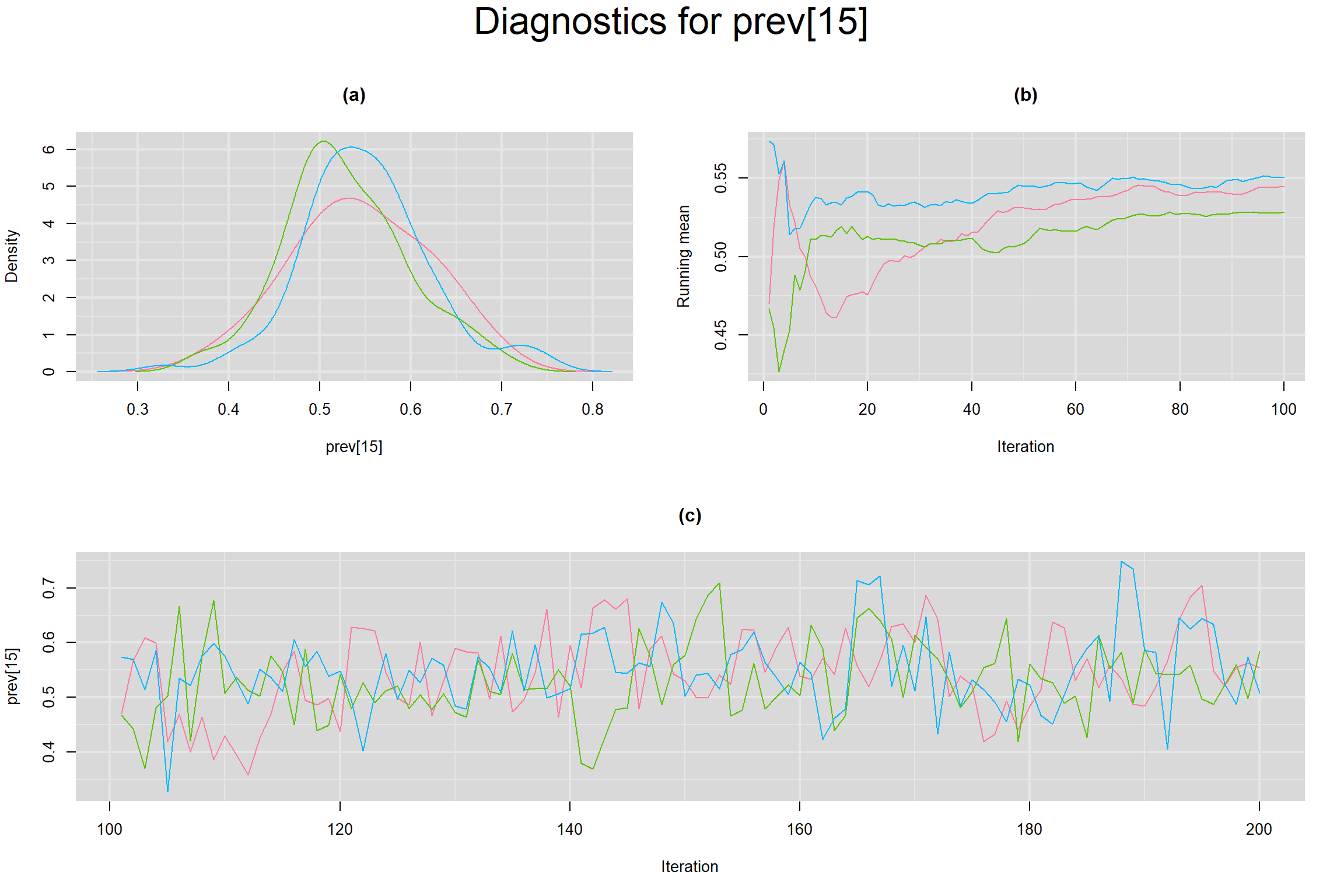
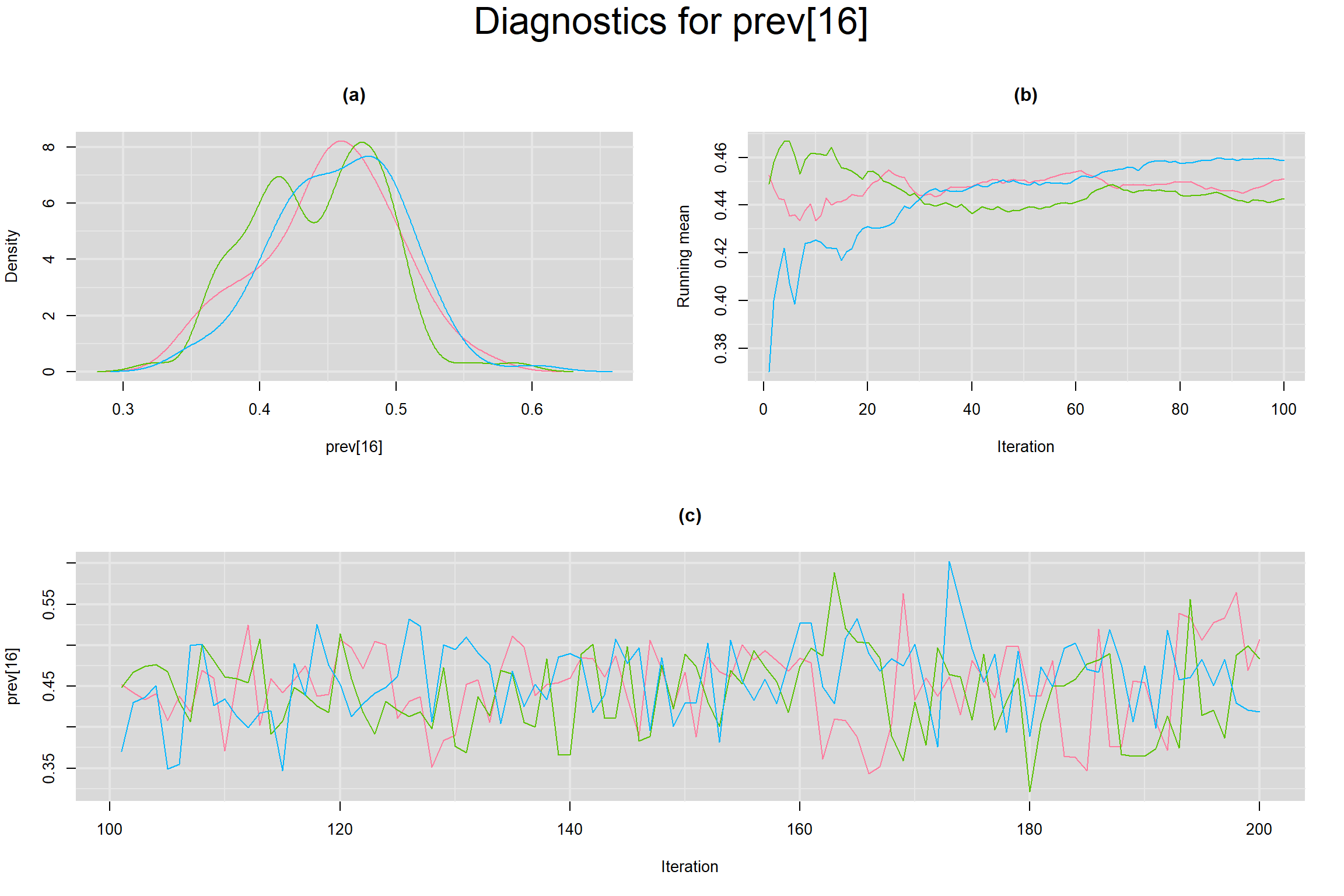
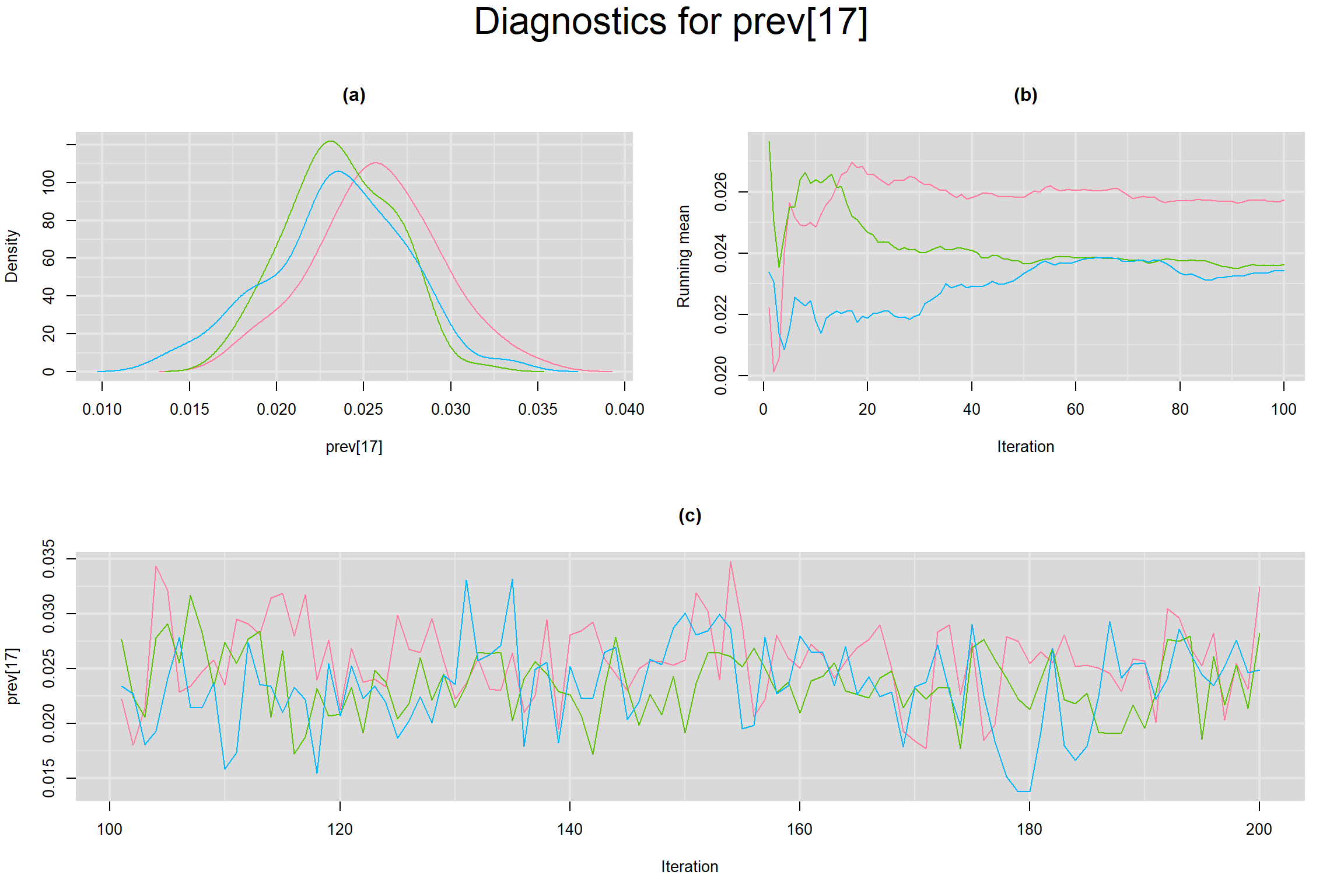
Visual inspection of convergence for key parameters can be studied below. For a given parameter, panel (a) shows posterior density plot; (b) the running posterior mean value; and (c) the history plot. Each chain is identified by a different color. Similar results from all3 chains would suggest the algorithm has converged.
INDEX TEST
PREDICTED SENSITIVITY AND SPECIFICITY IN A FUTURE STUDY
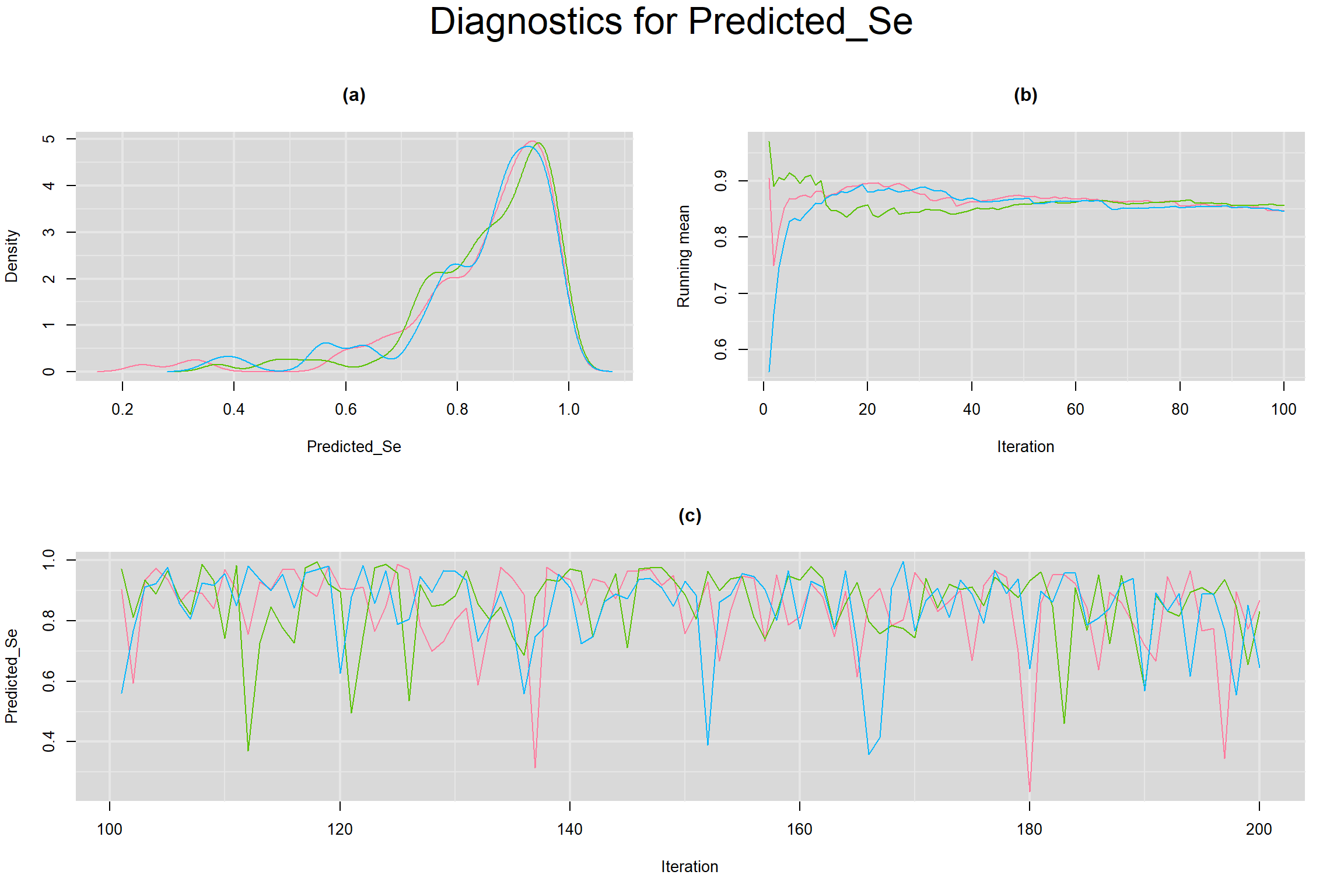
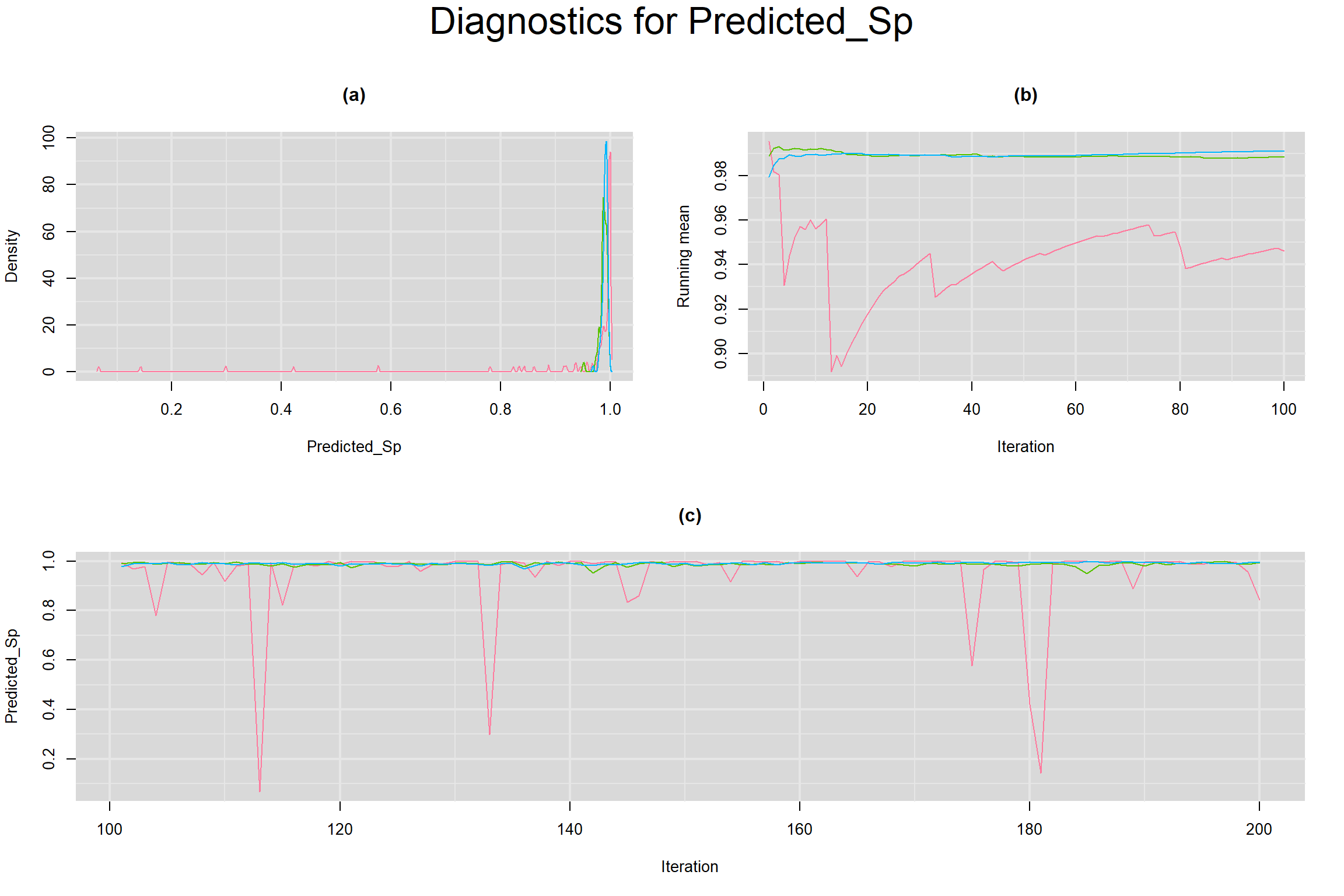
SUMMARY SENSITIVITY AND SPECIFICITY ACROSS ALL STUDIES
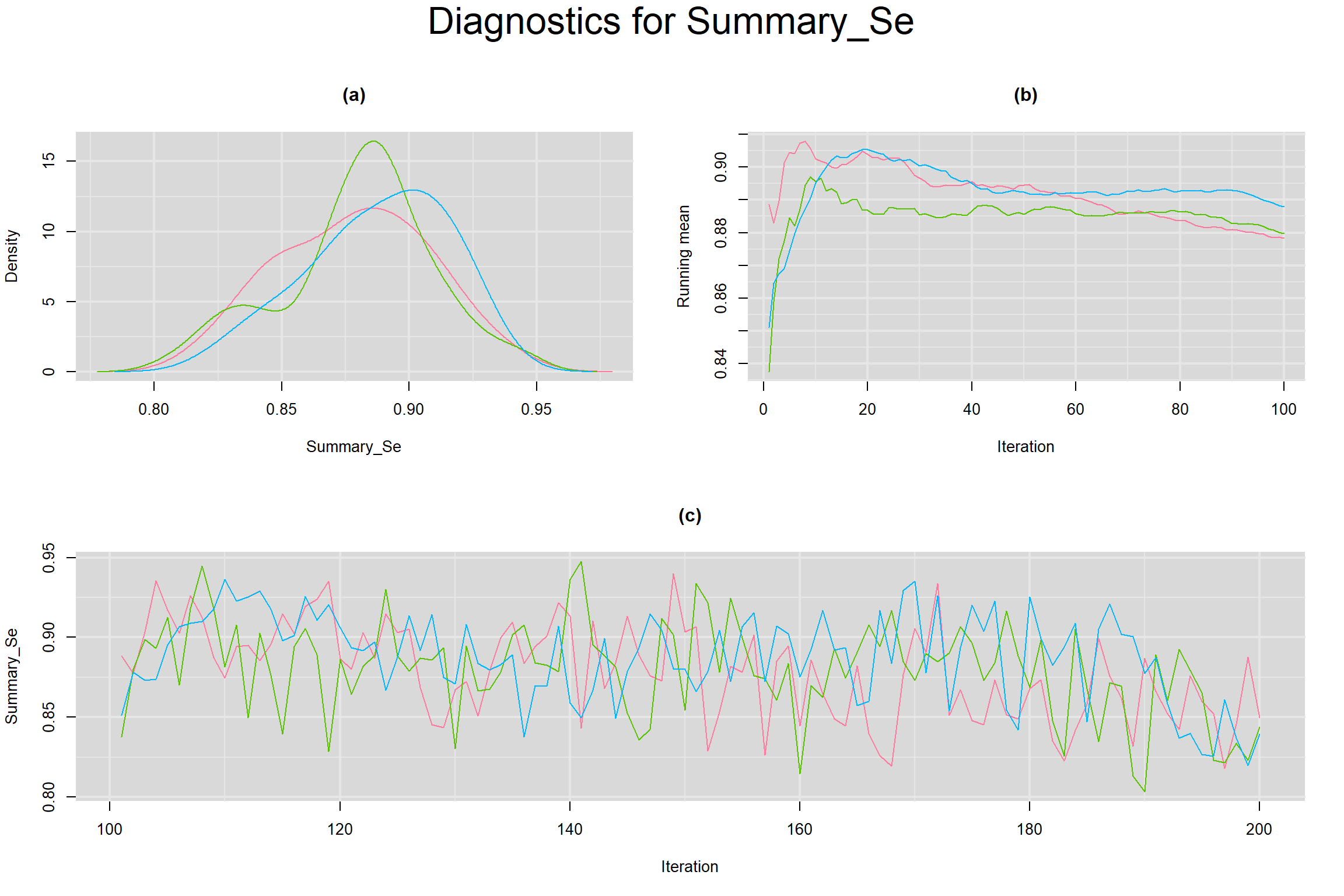
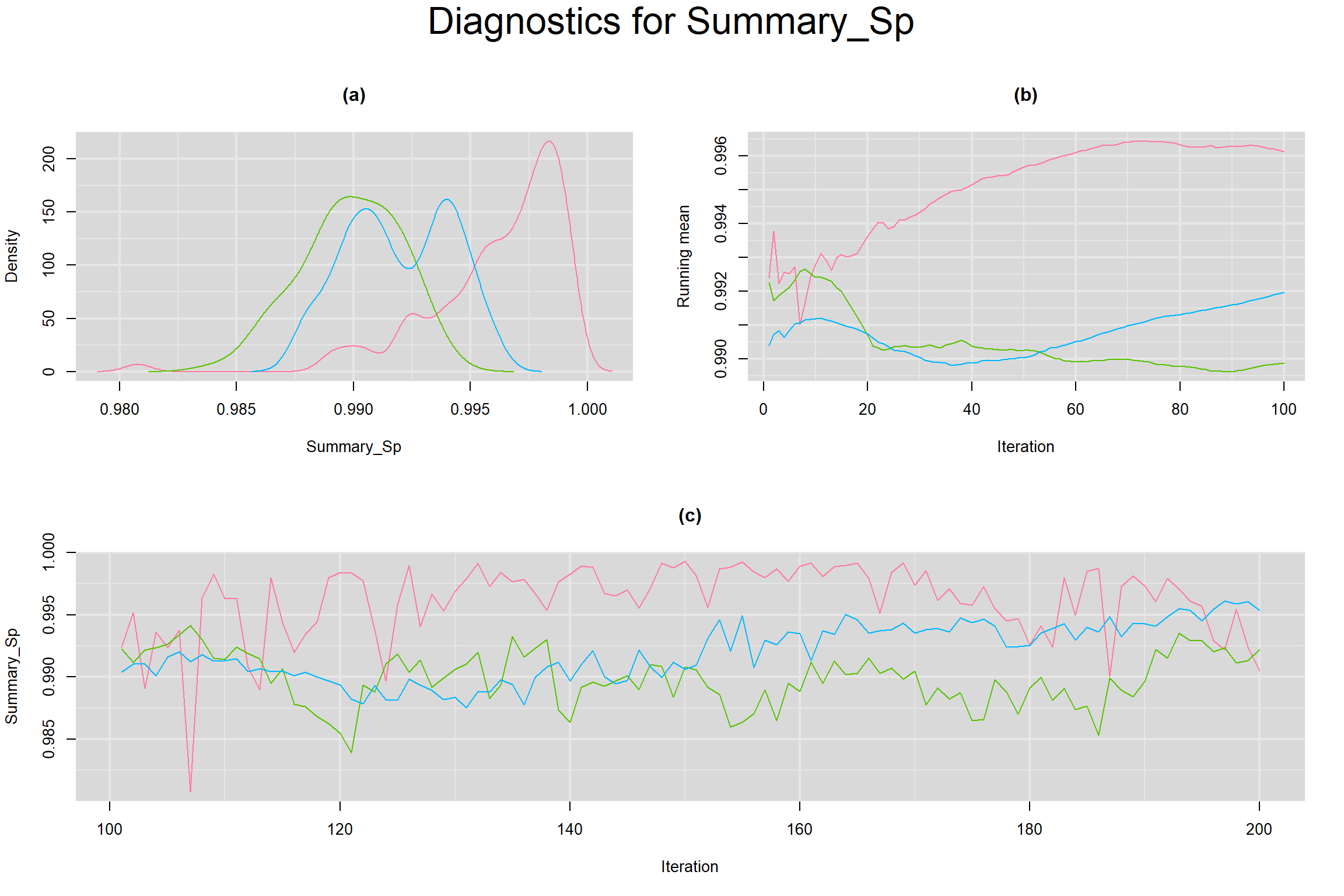
MEAN LOGIT-TRANSFORMED SENSITIVITY AND SPECIFICITY

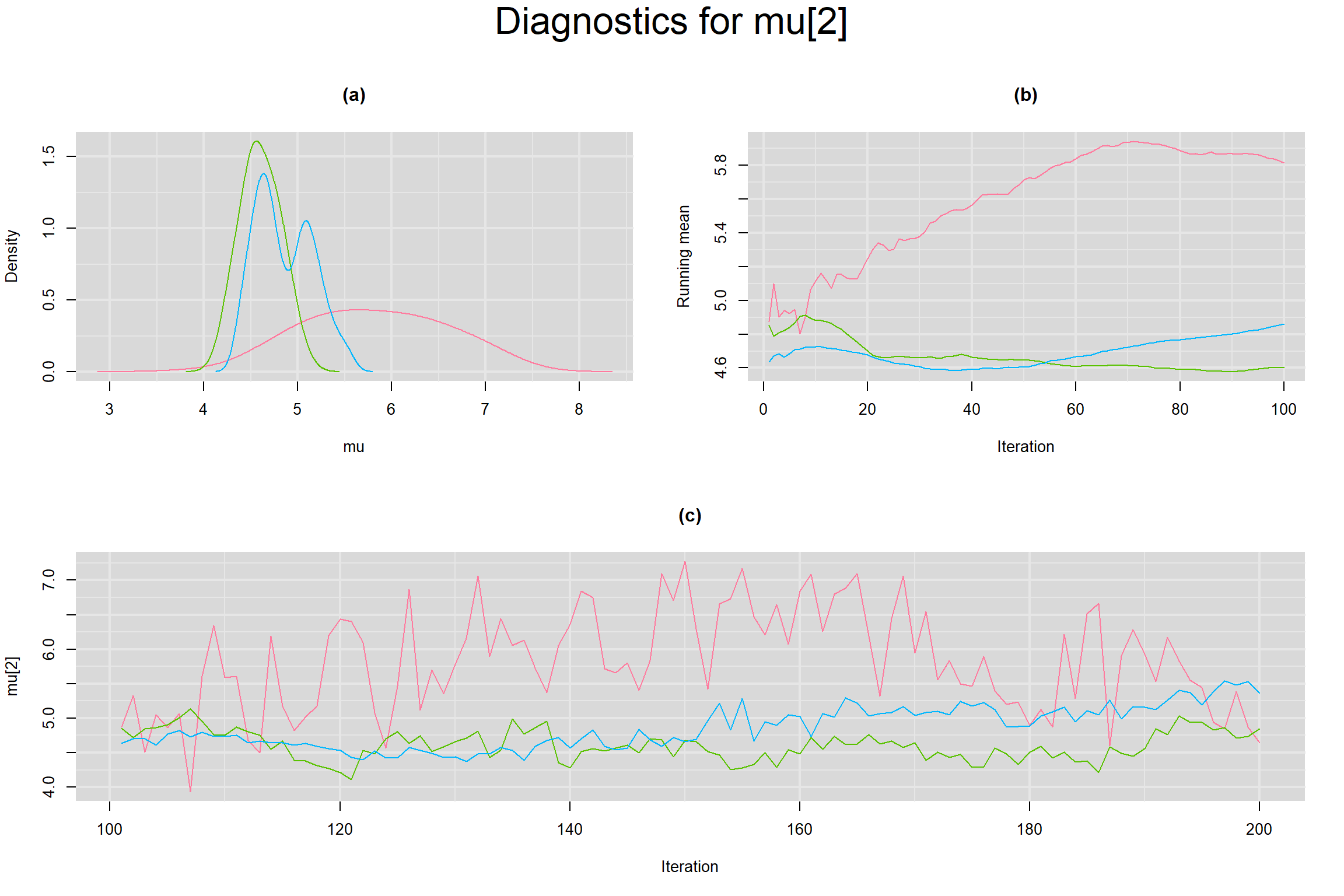
CORRELATION BETWEEN MEAN LOGIT-TRANSFORMED SENSITIVITY AND MEAN LOGIT-TRANSFORMED SPECIFICITY
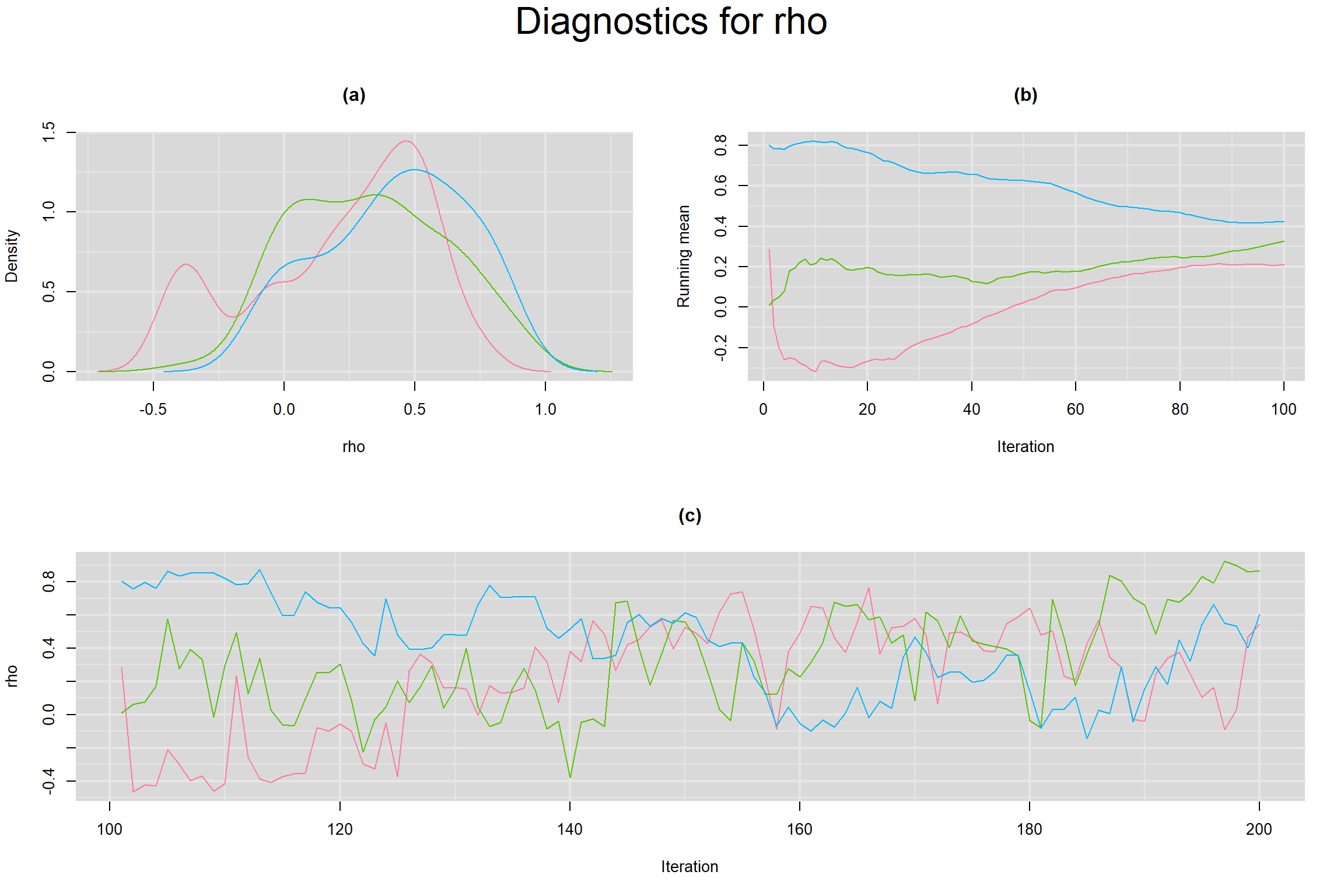
SENSITIVITY IN INDIVIDUAL STUDIES
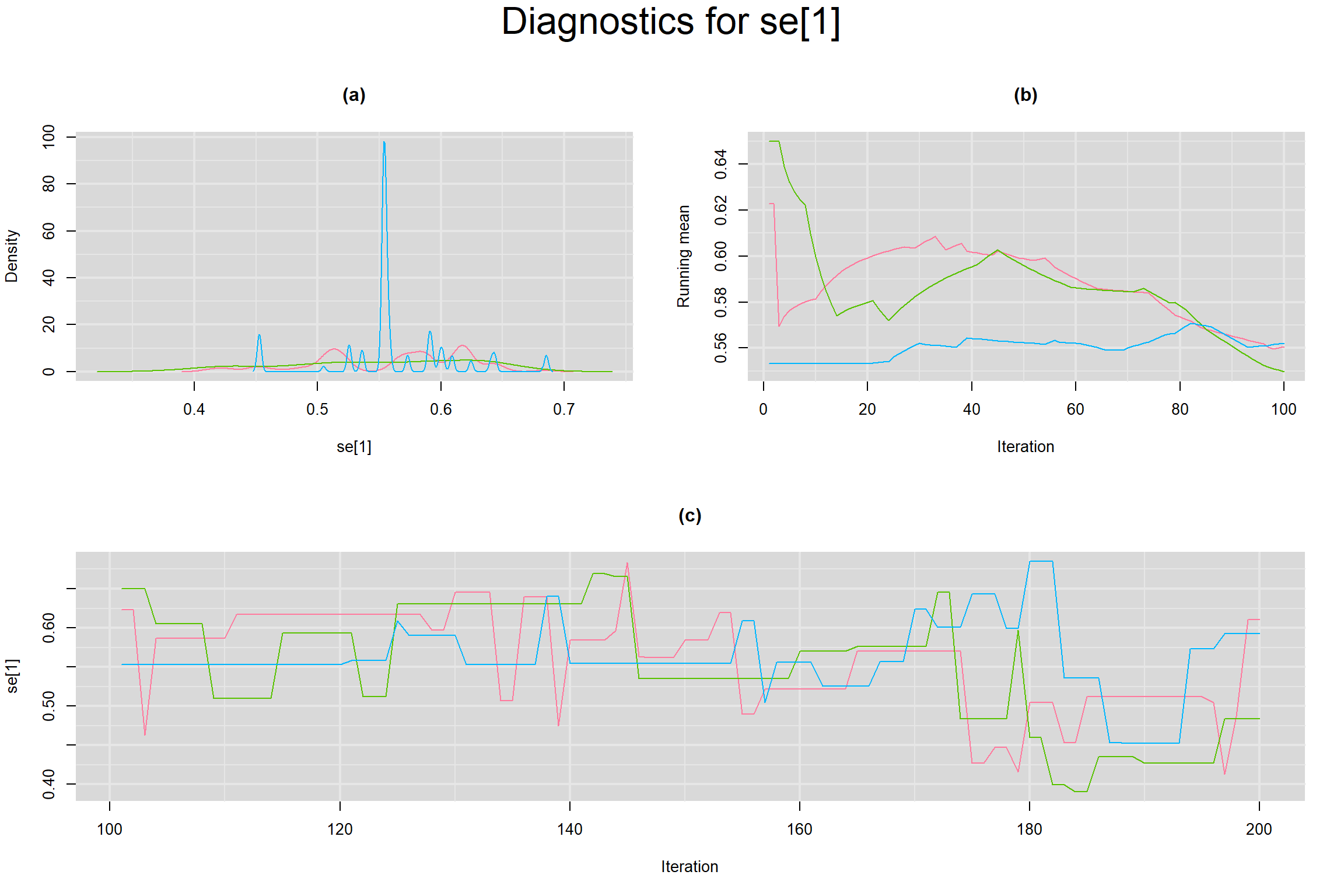
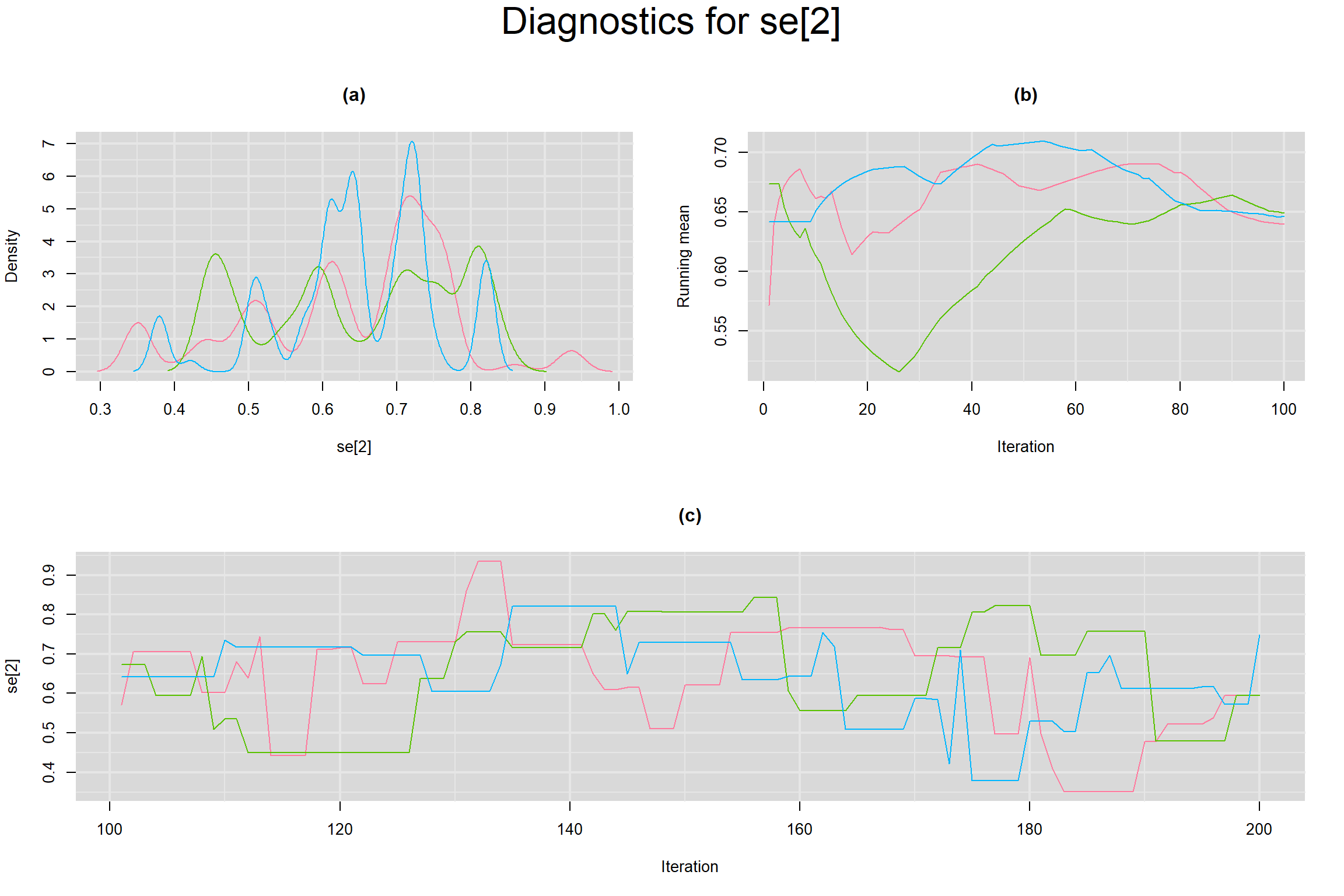
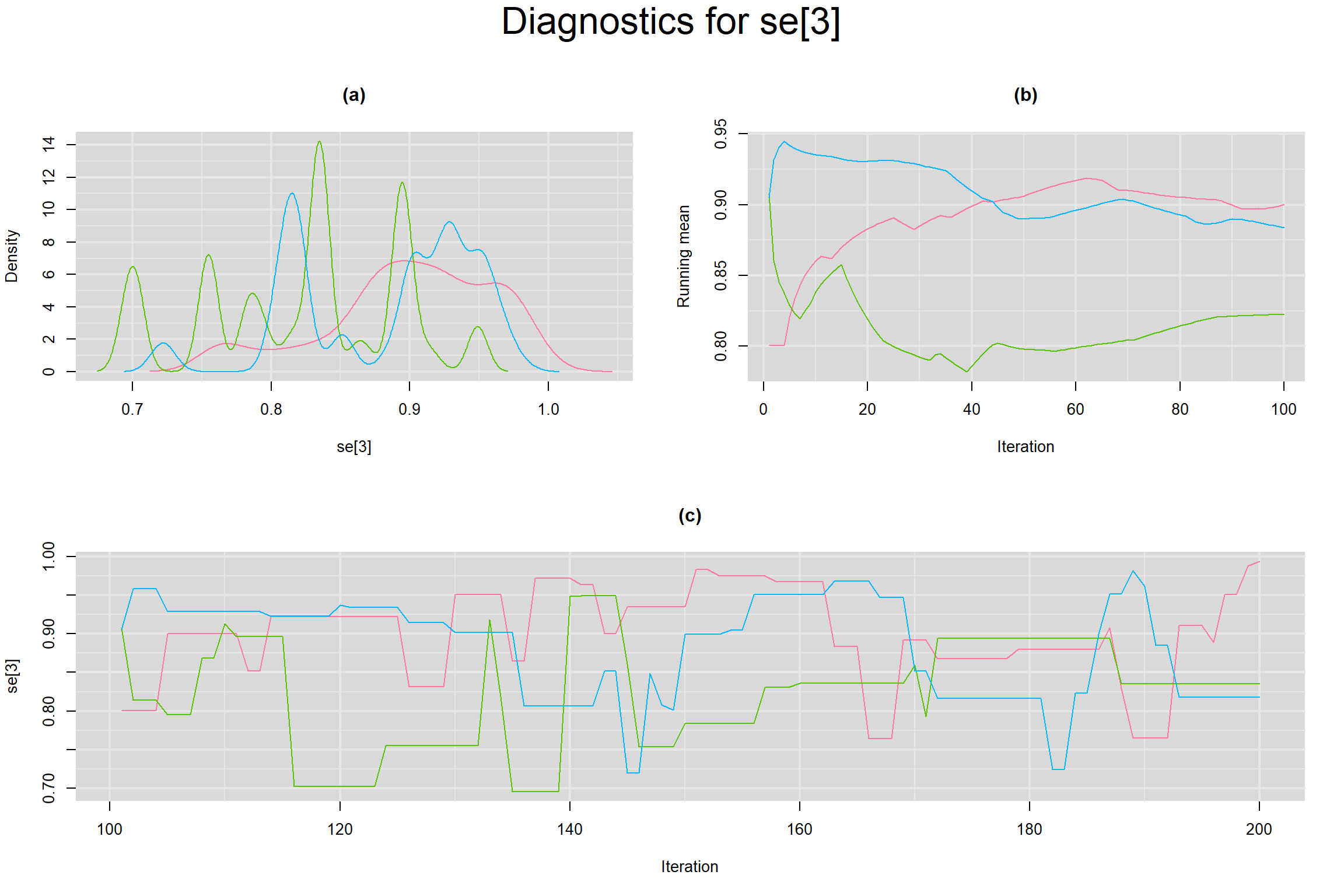
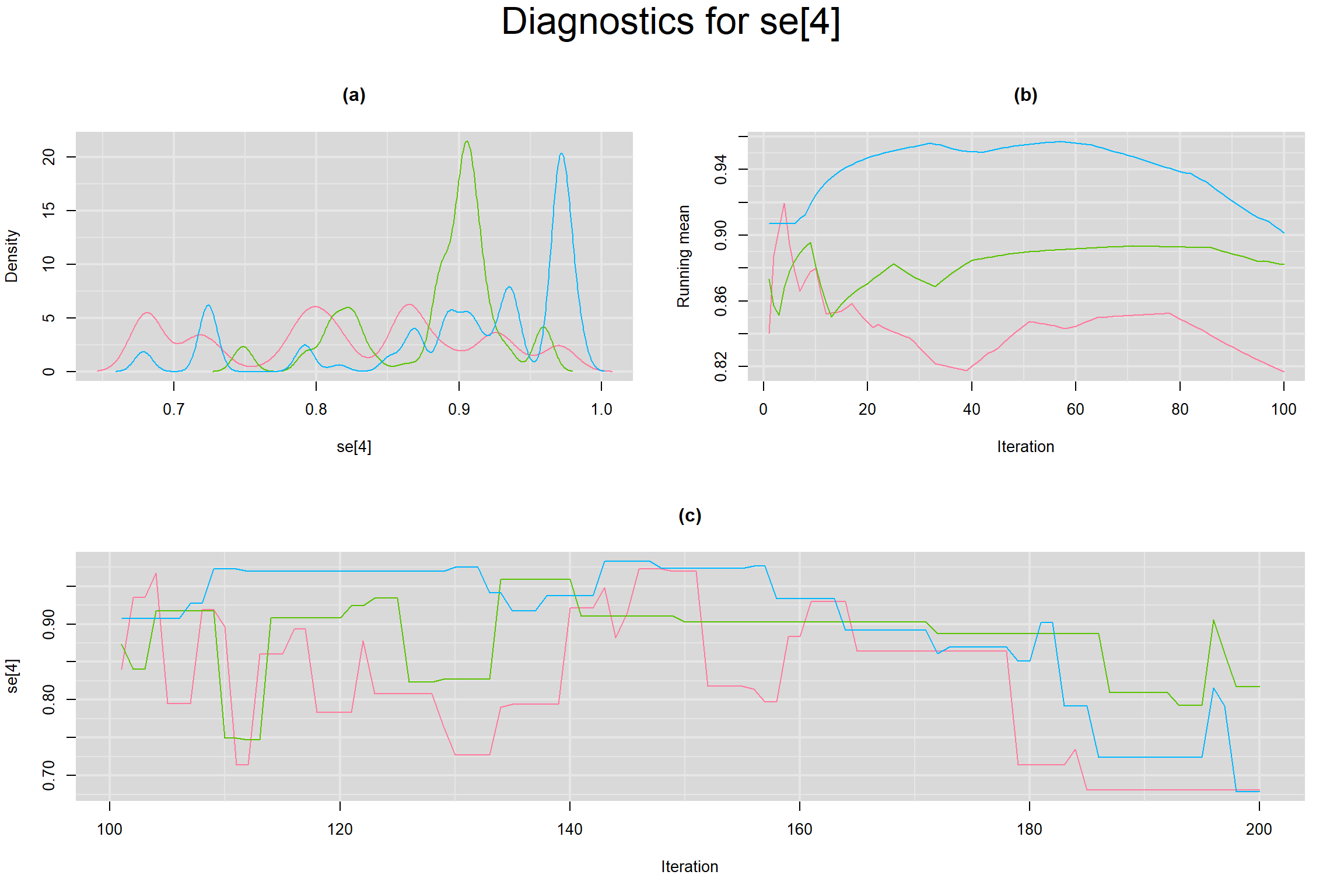
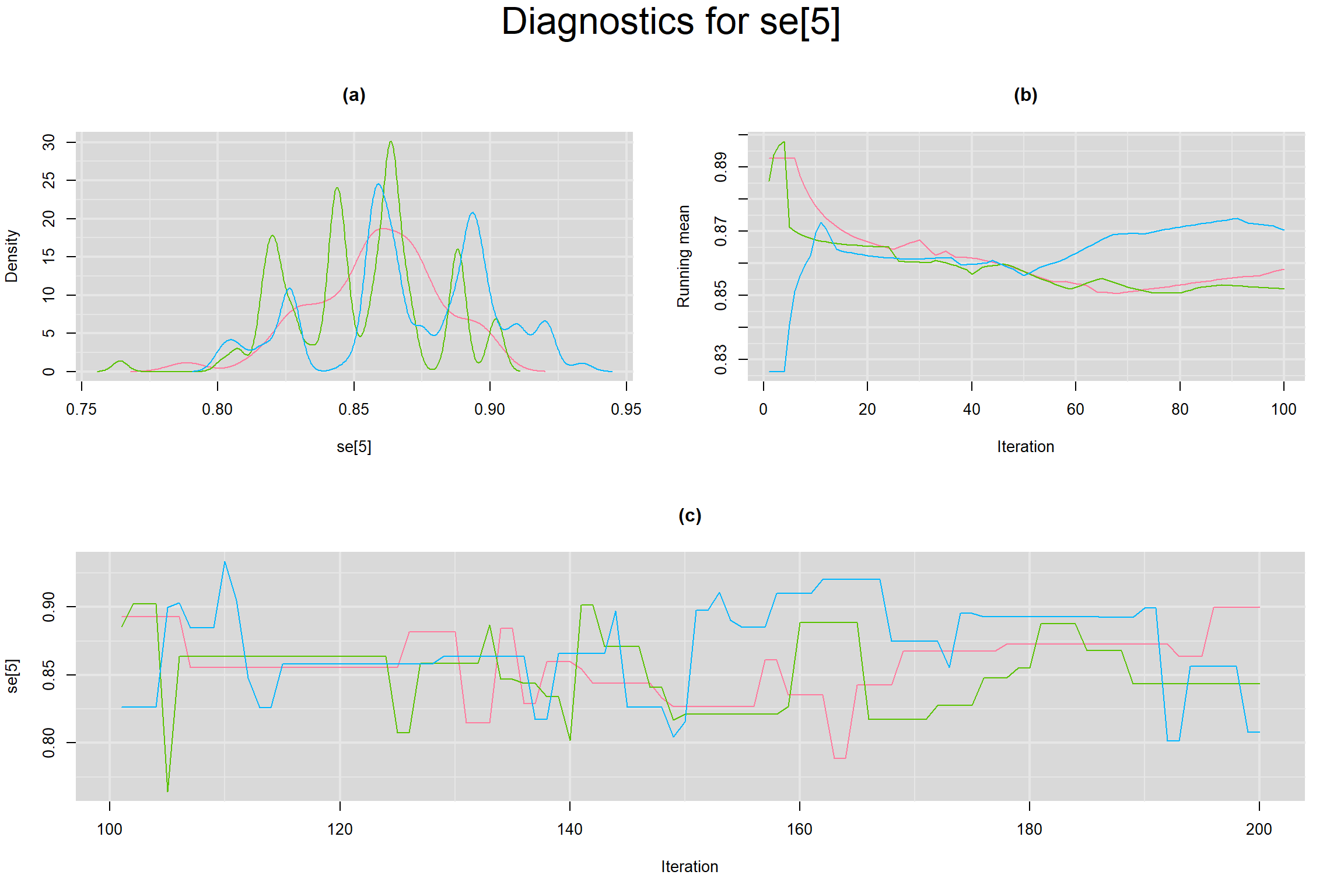
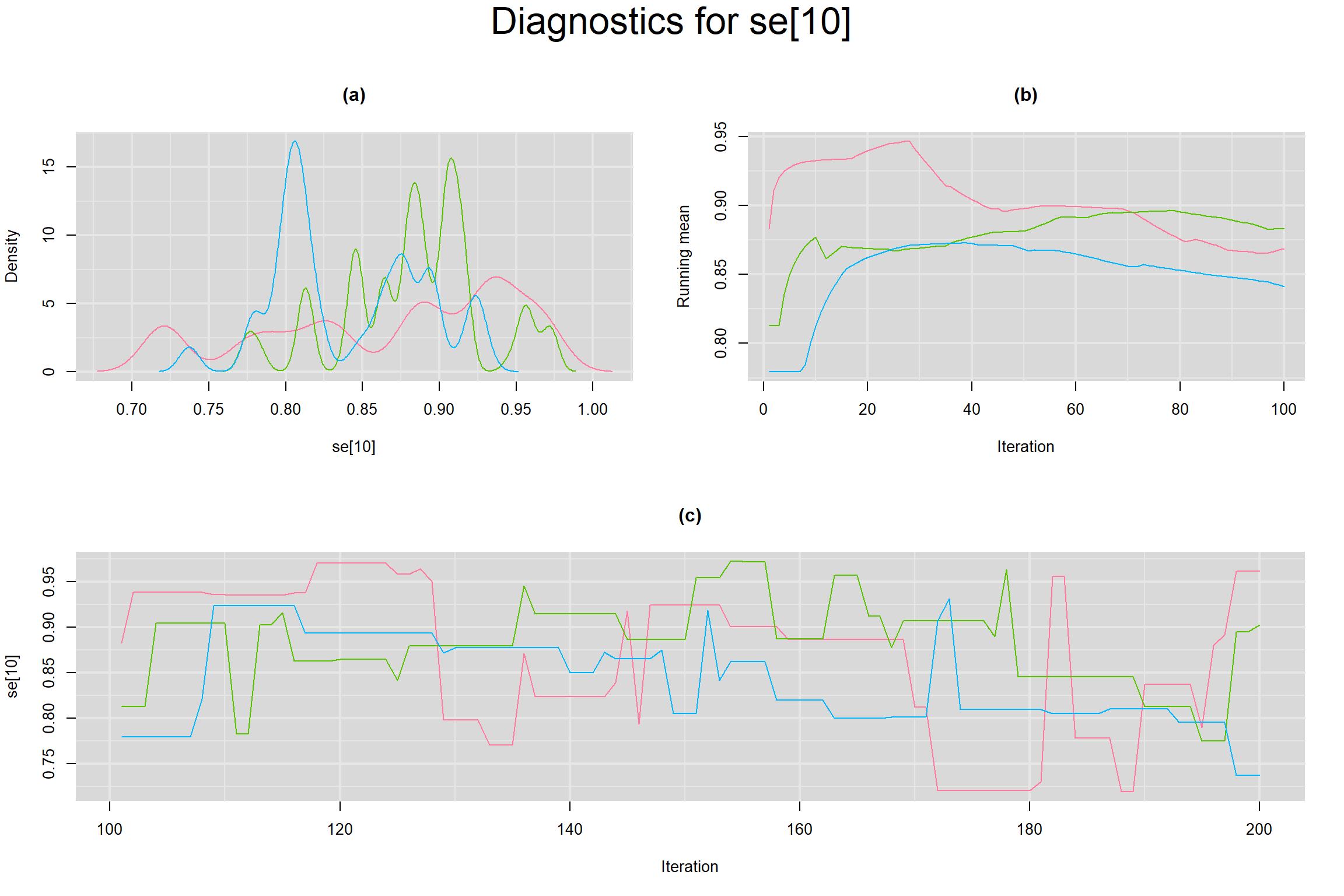
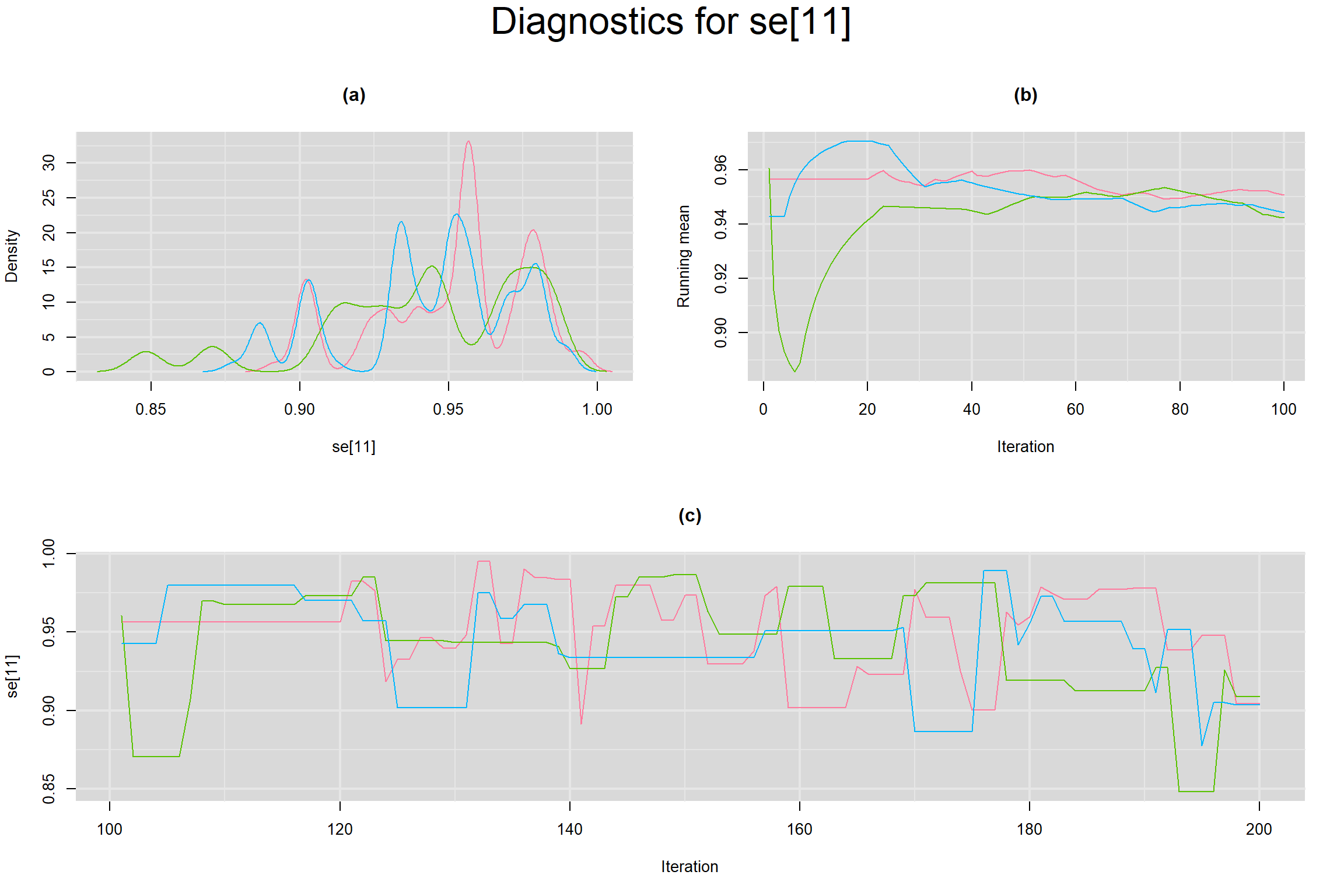
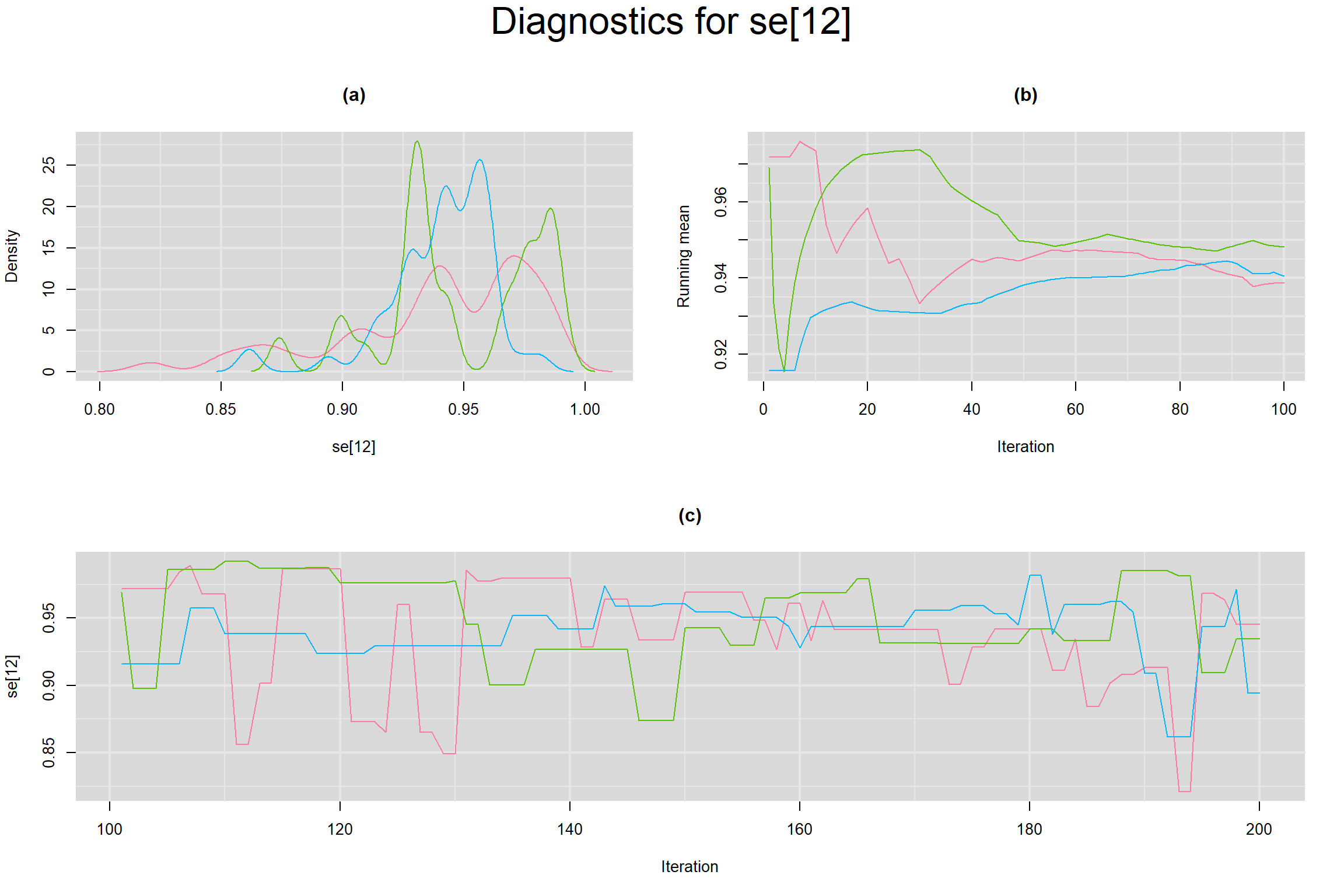

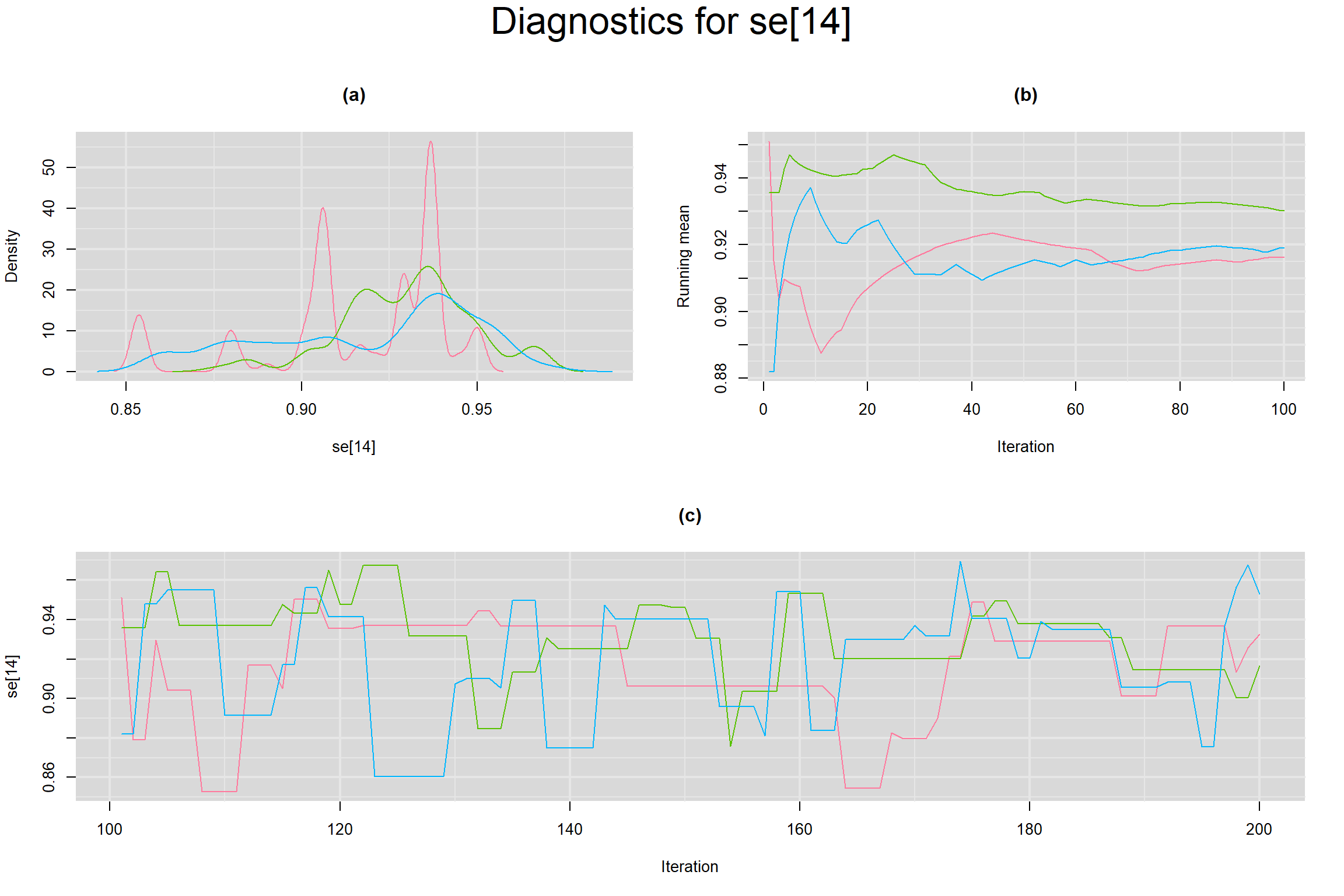
SPECIFICITY IN INDIVIDUAL STUDIES


BETWEEN-STUDY VARIANCE IN THE LOGIT-TRANSFORMED SENSITIVITY AND SPECIFICITY
BETWEEN-STUDY STANDARD DEVIATION IN THE LOGIT-TRANSFORMED SENSITIVITY AND SPECIFICITY
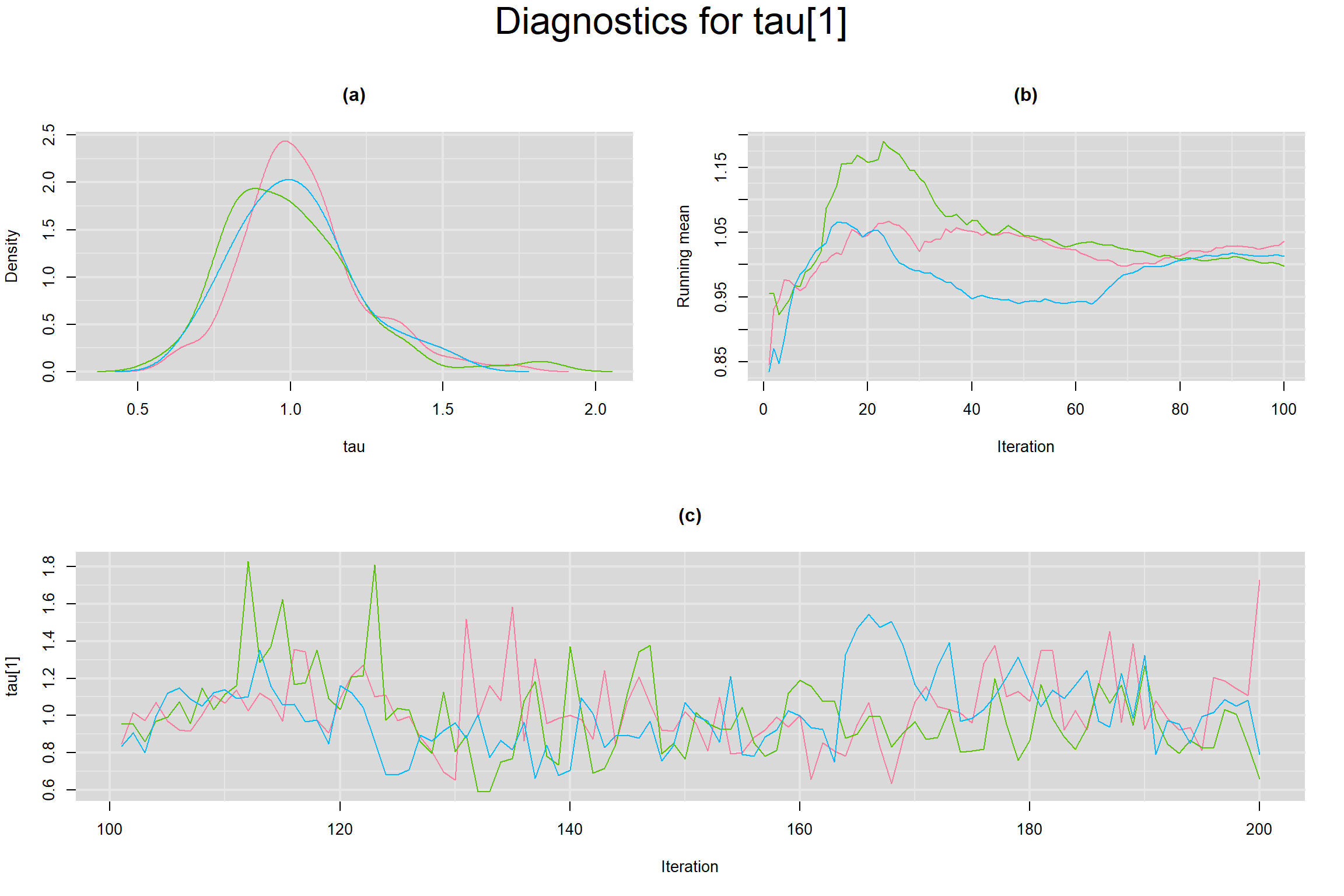
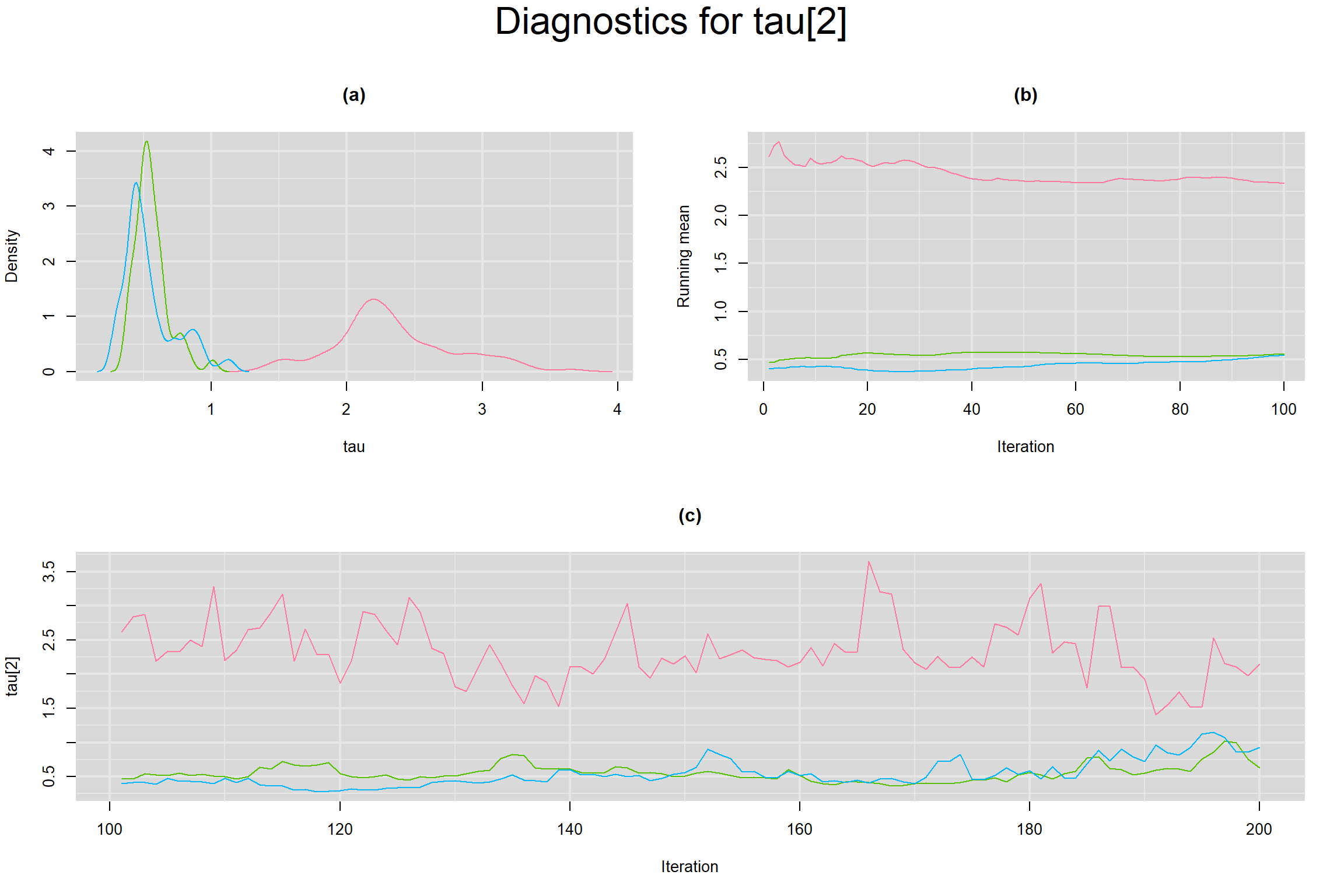
BETWEEN-STUDY PRECISION IN THE LOGIT-TRANSFORMED SENSITIVITY AND SPECIFICITY
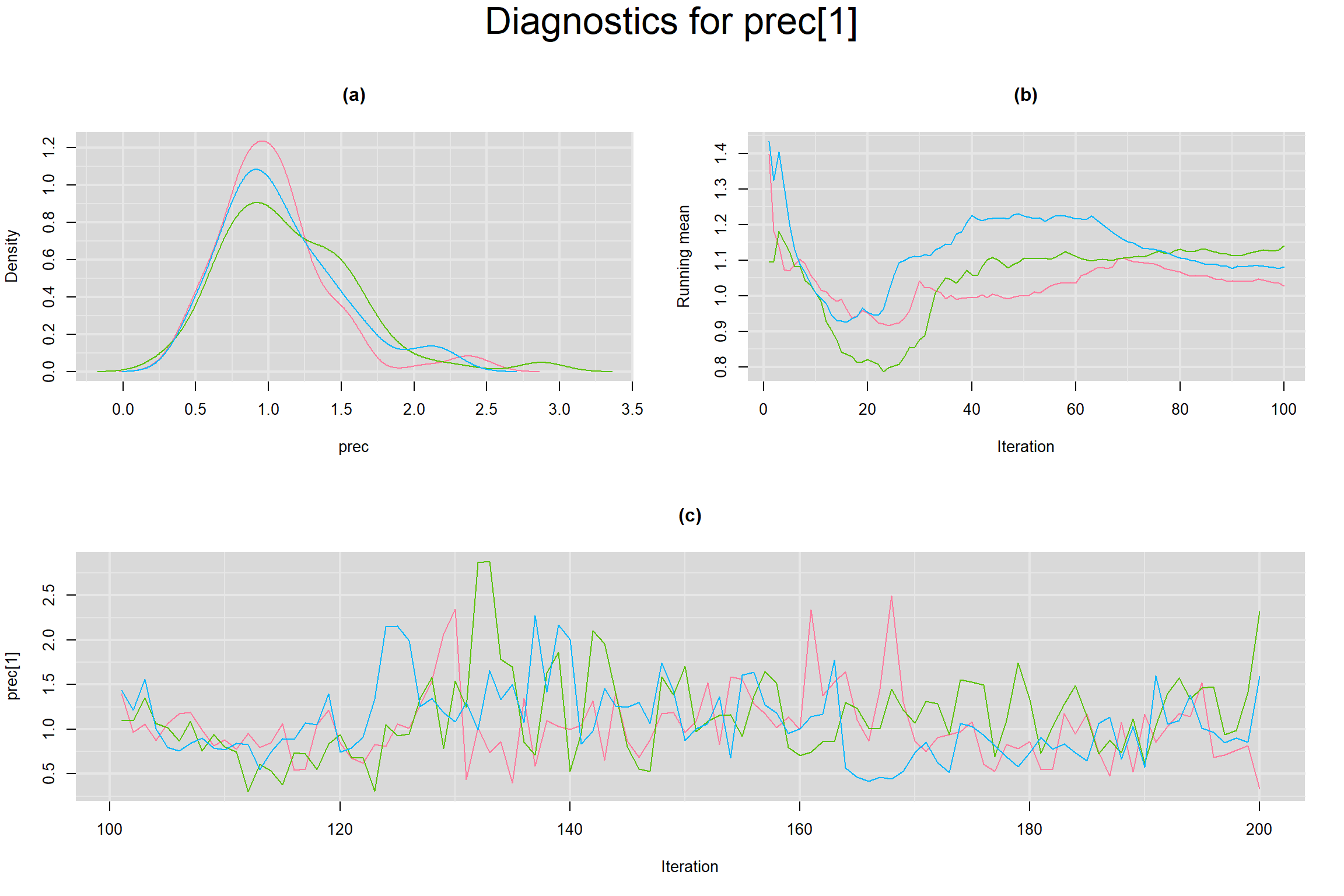
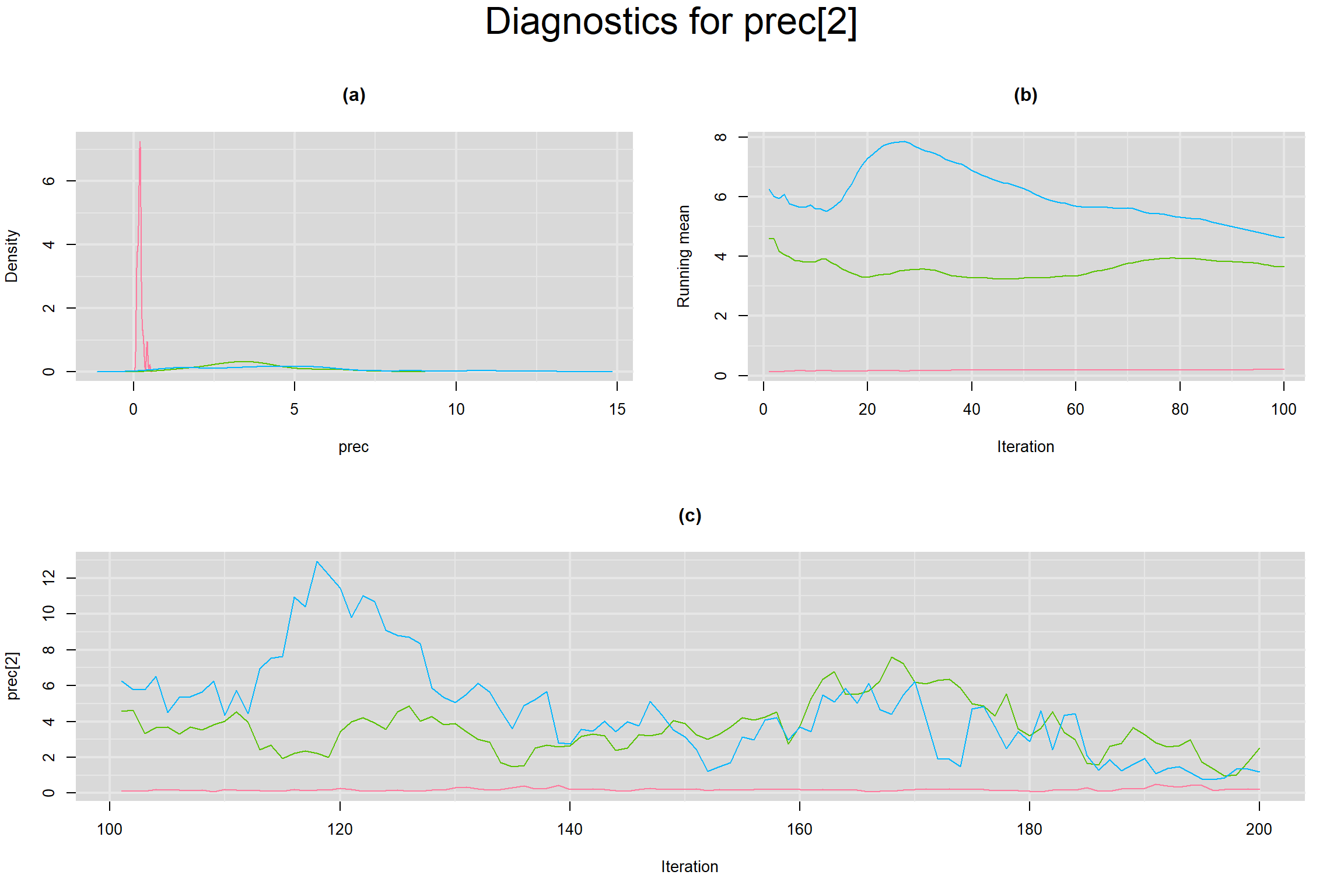
REFERENCE TEST
PREDICTED SENSITIVITY AND SPECIFICITY IN A FUTURE STUDY
SUMMARY SENSITIVITY AND SPECIFICITY ACROSS ALL STUDIES
MEAN LOGIT-TRANSFORMED SENSITIVITY AND SPECIFICITY
CORRELATION BETWEEN MEAN LOGIT-TRANSFORMED SENSITIVITY AND MEAN LOGIT-TRANSFORMED SPECIFICITY
SENSITIVITY IN INDIVIDUAL STUDIES
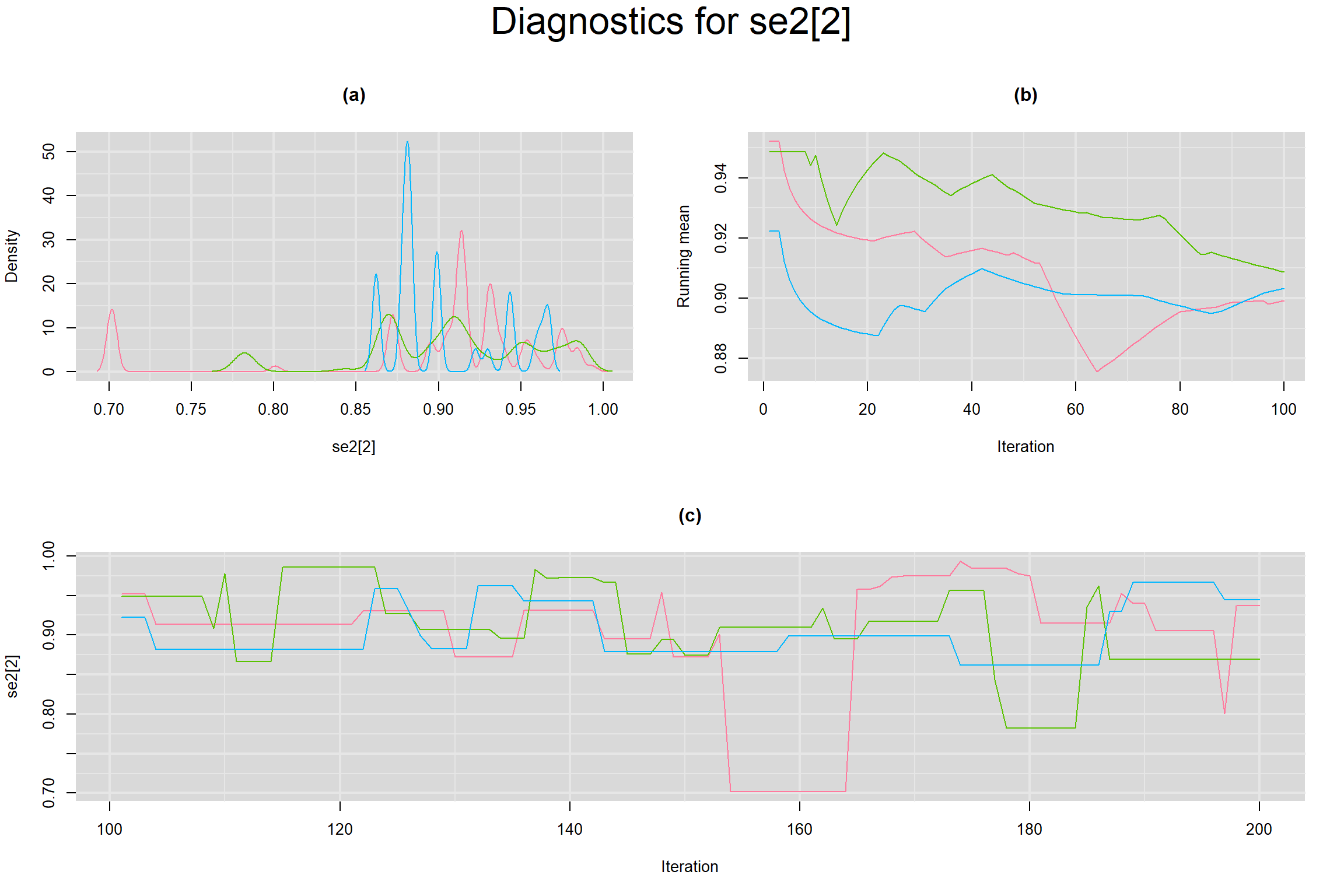
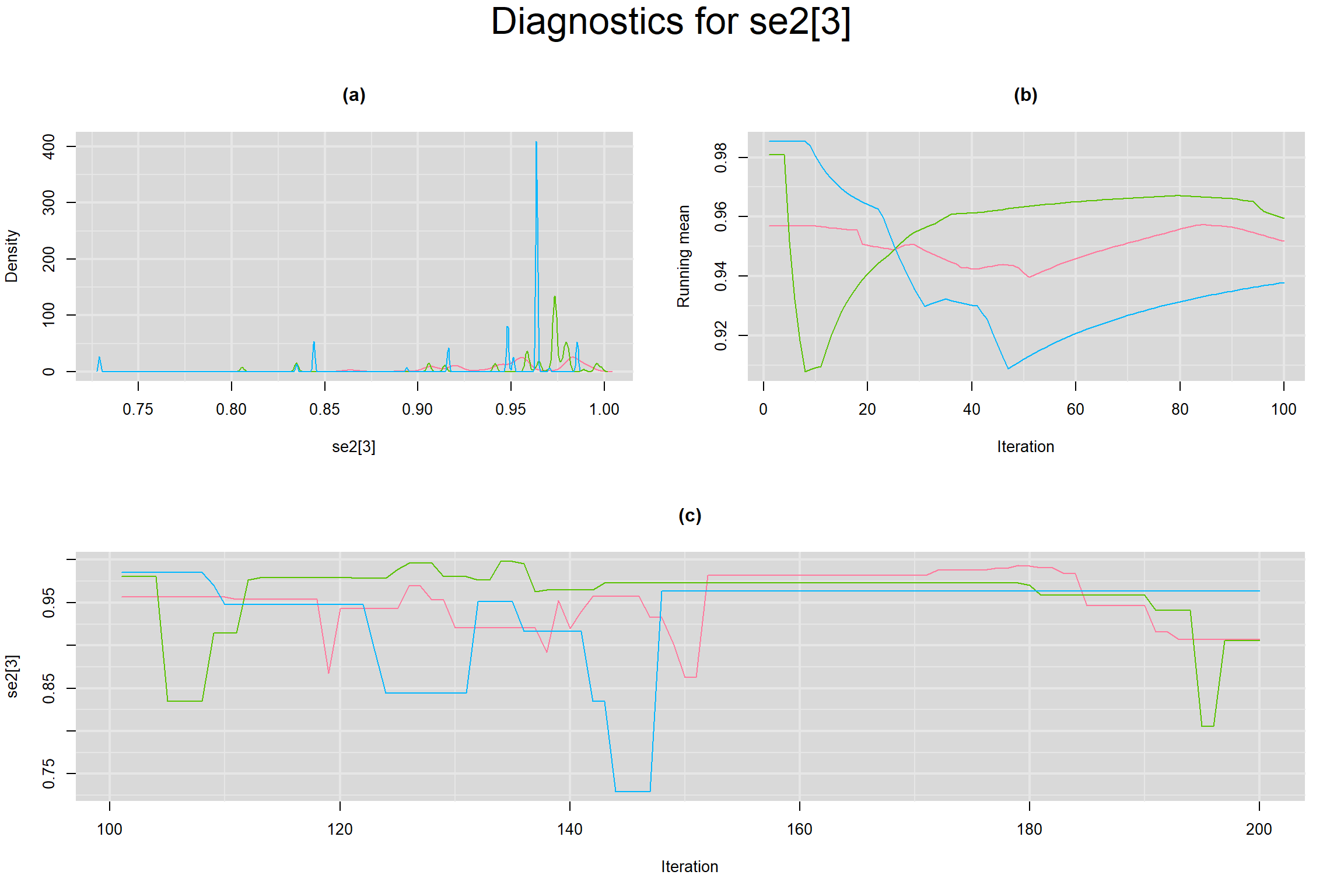
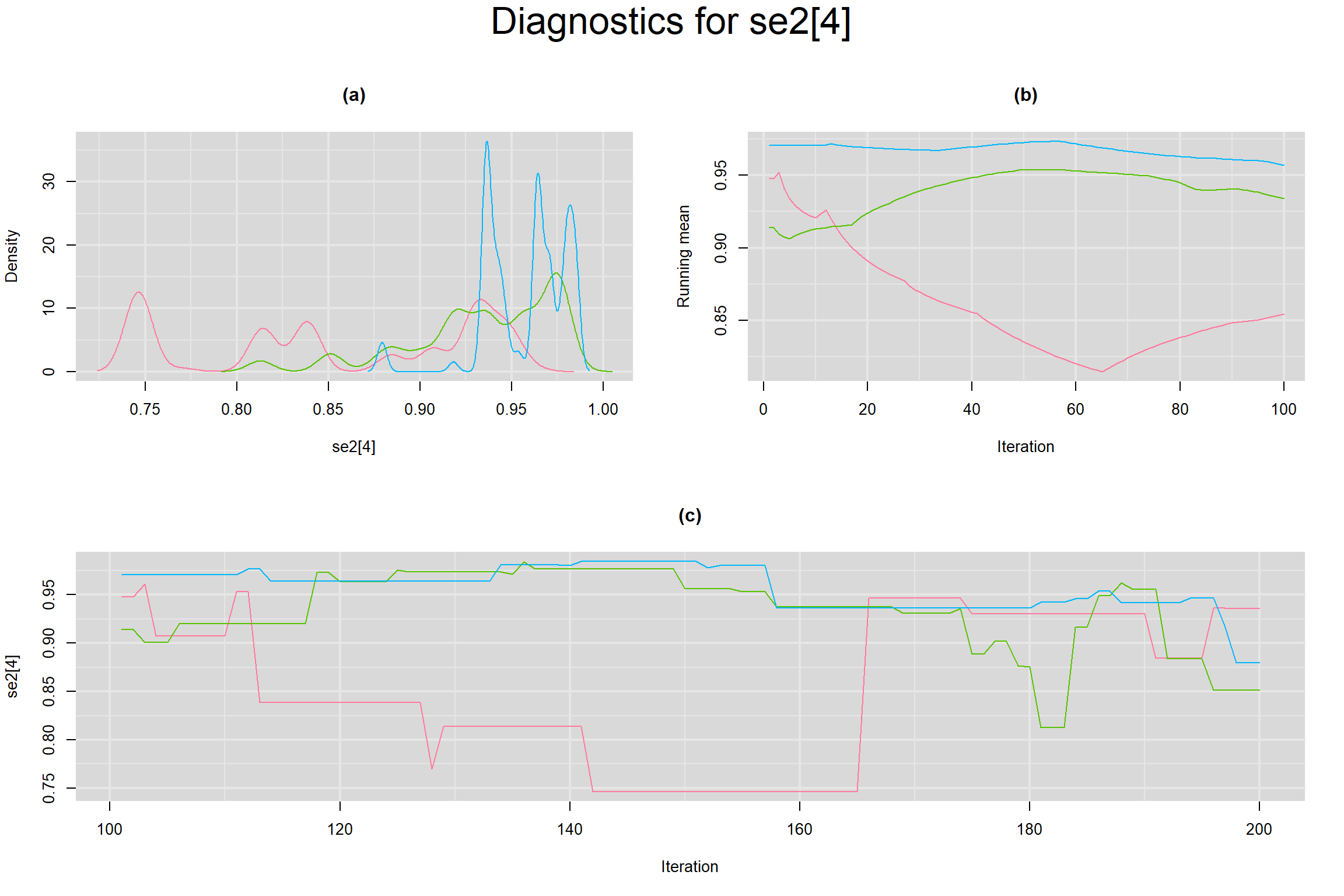
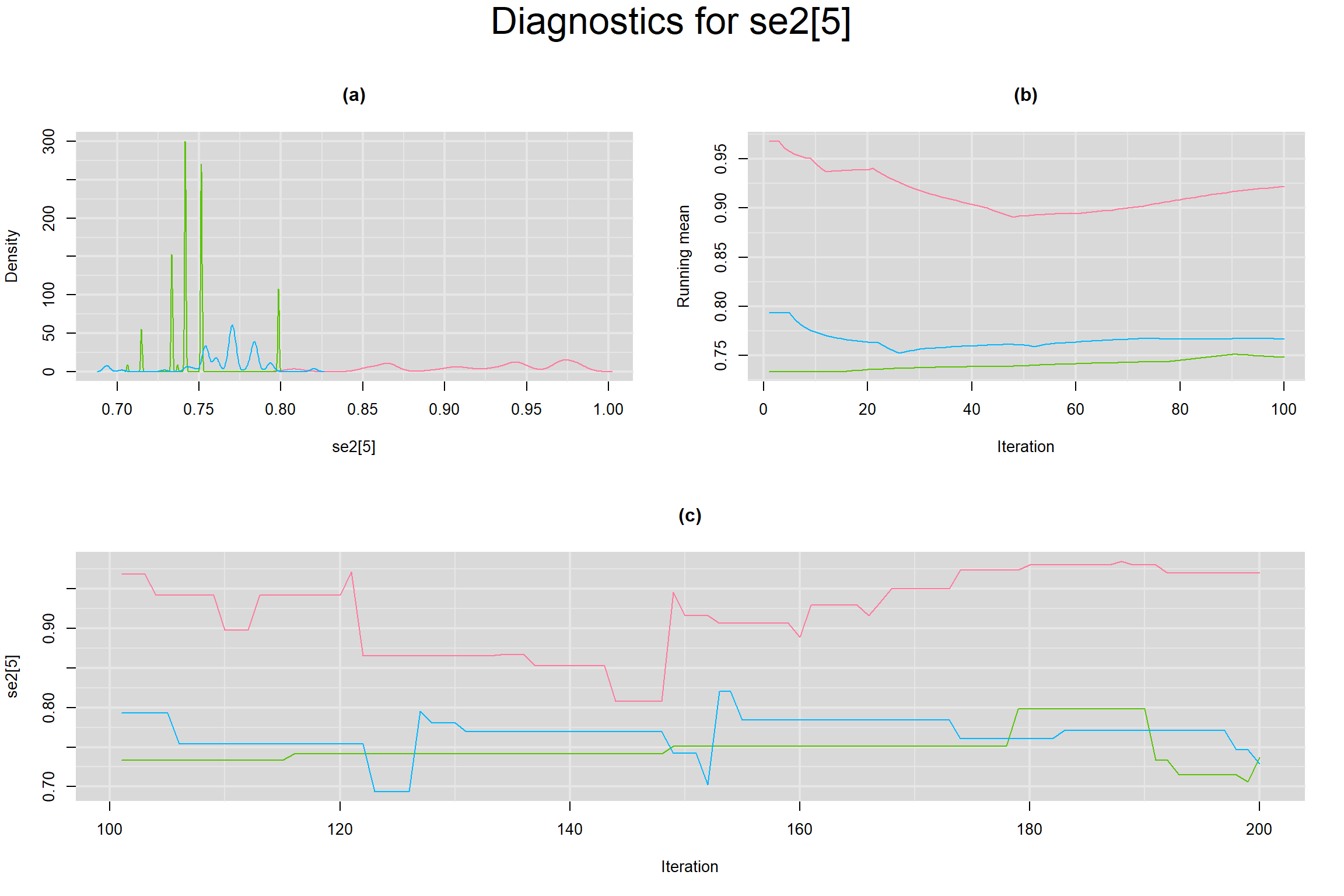
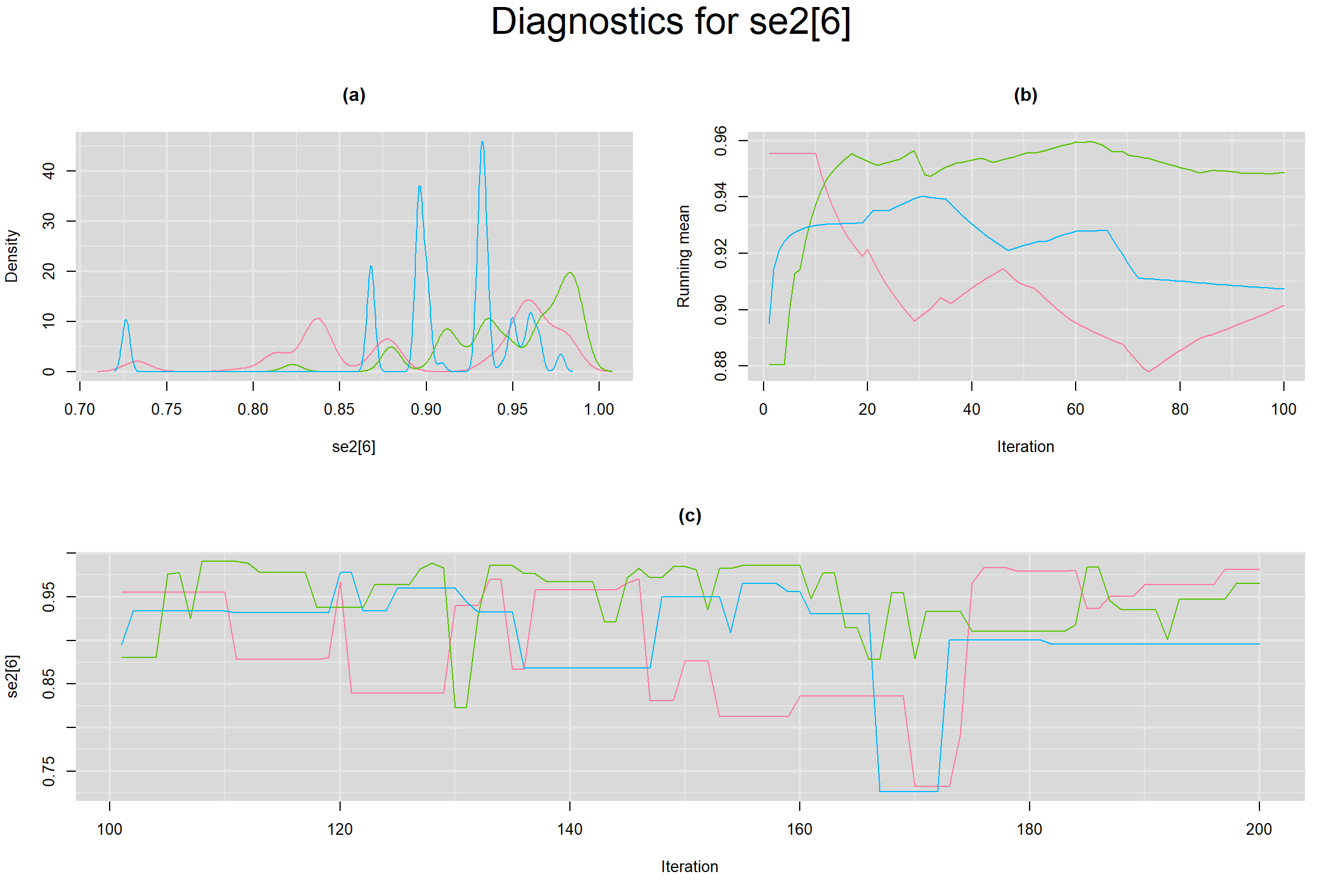
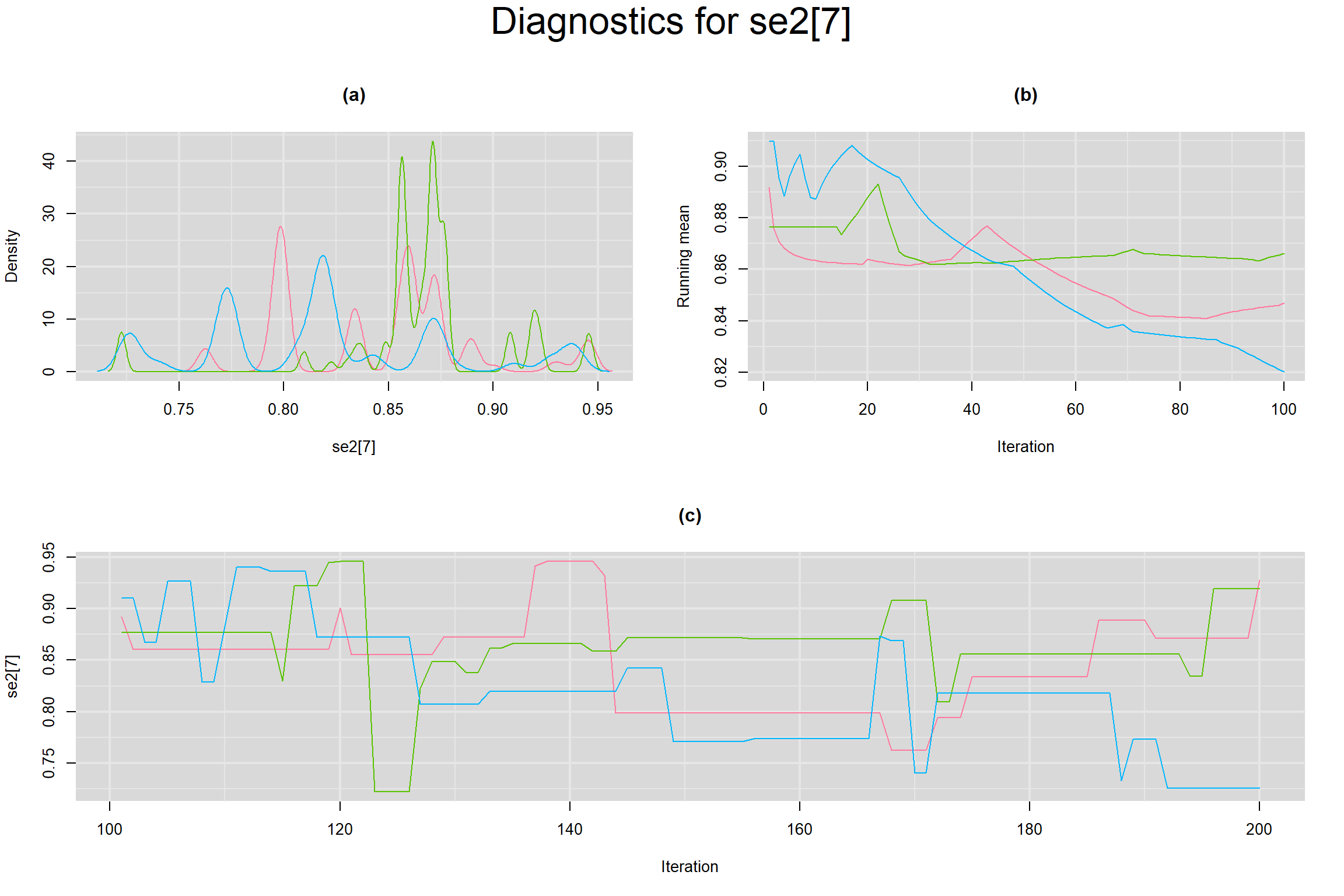
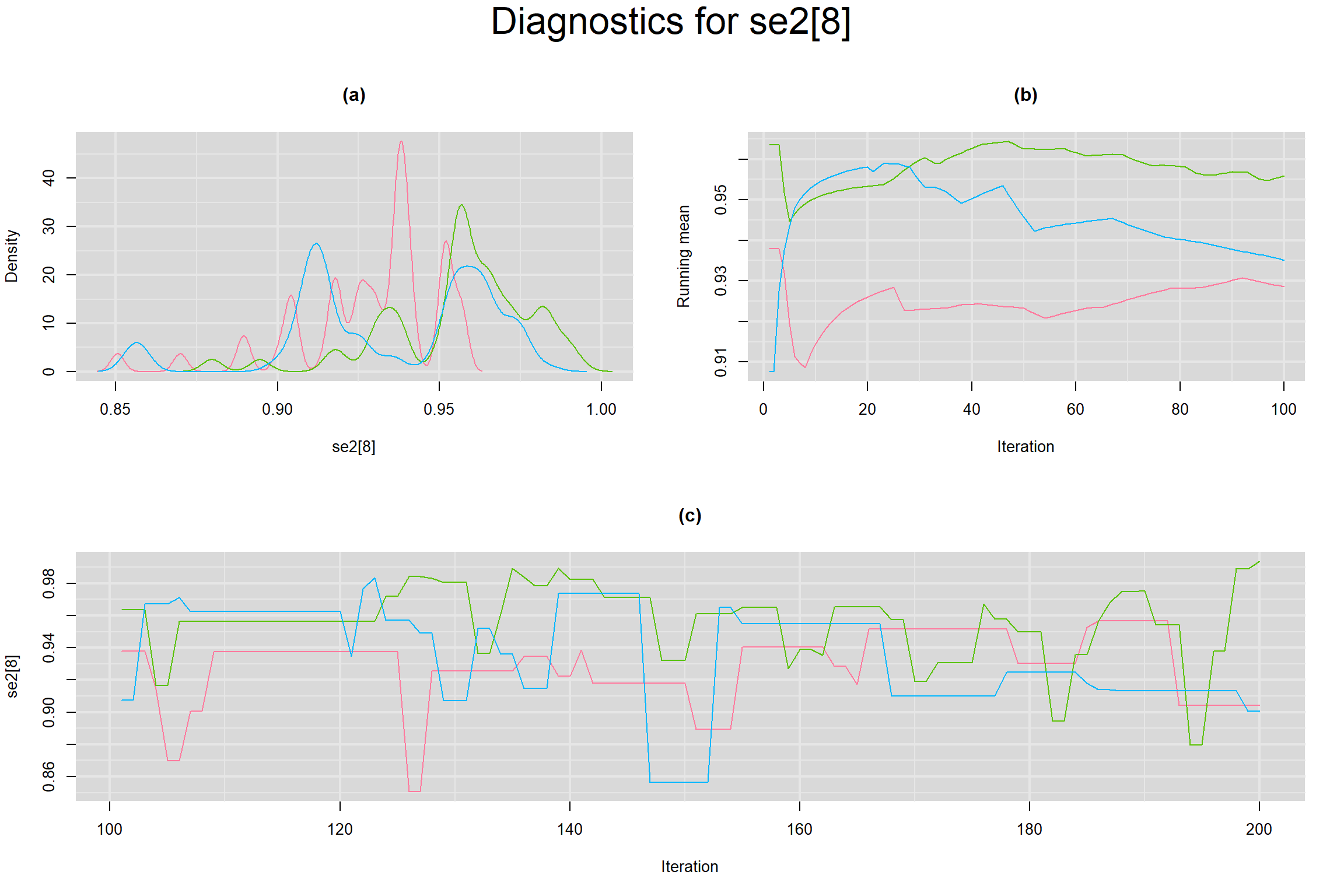
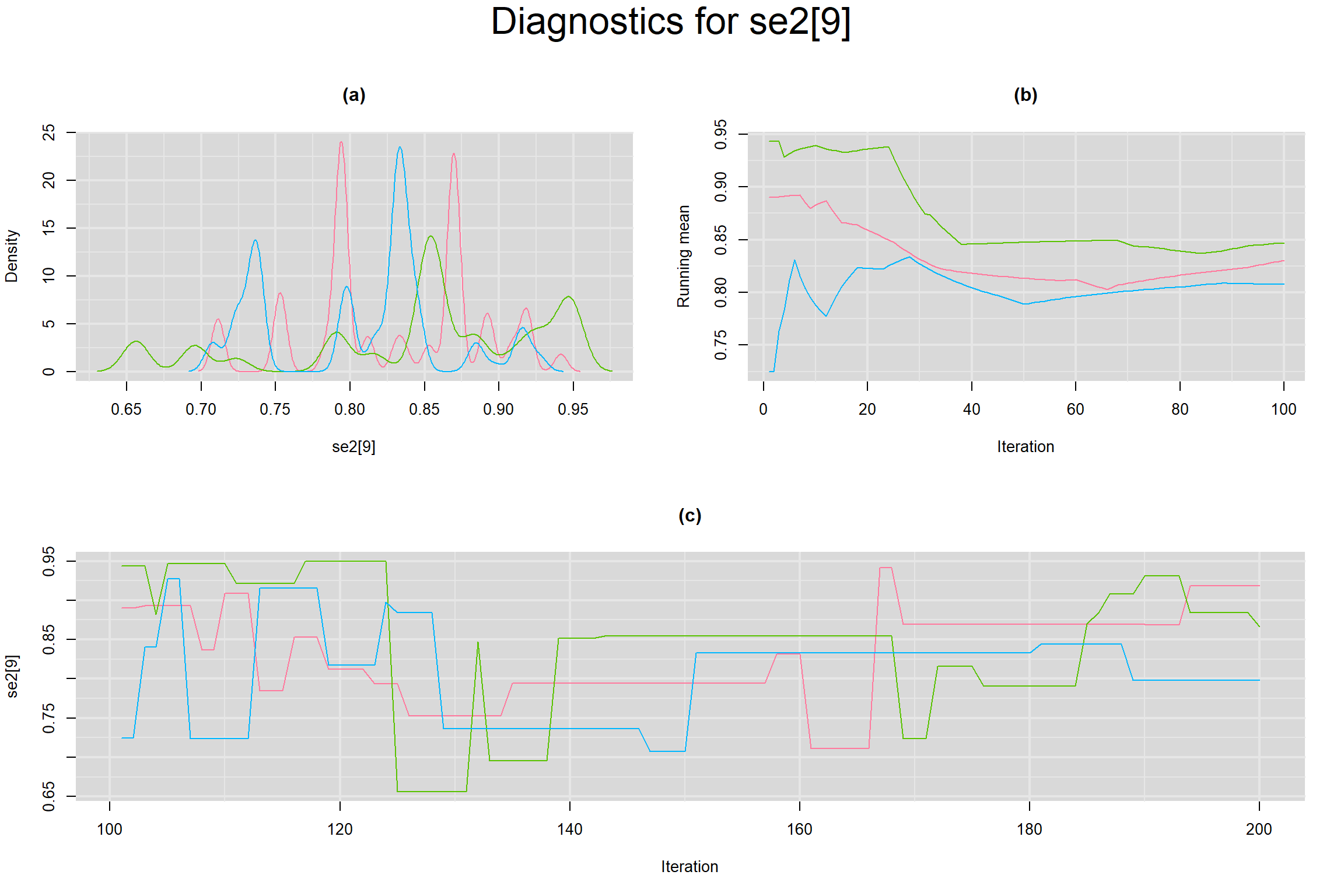
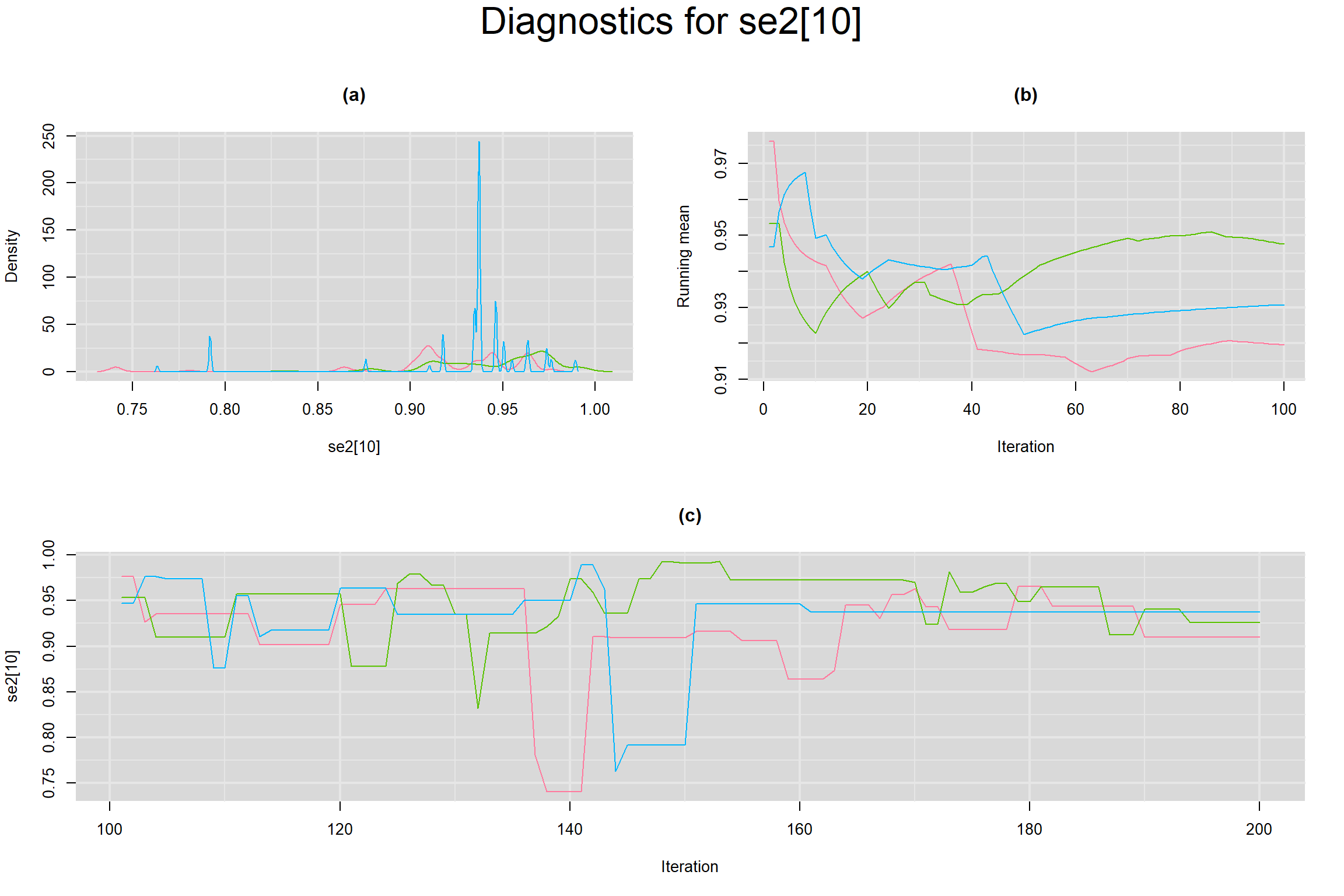
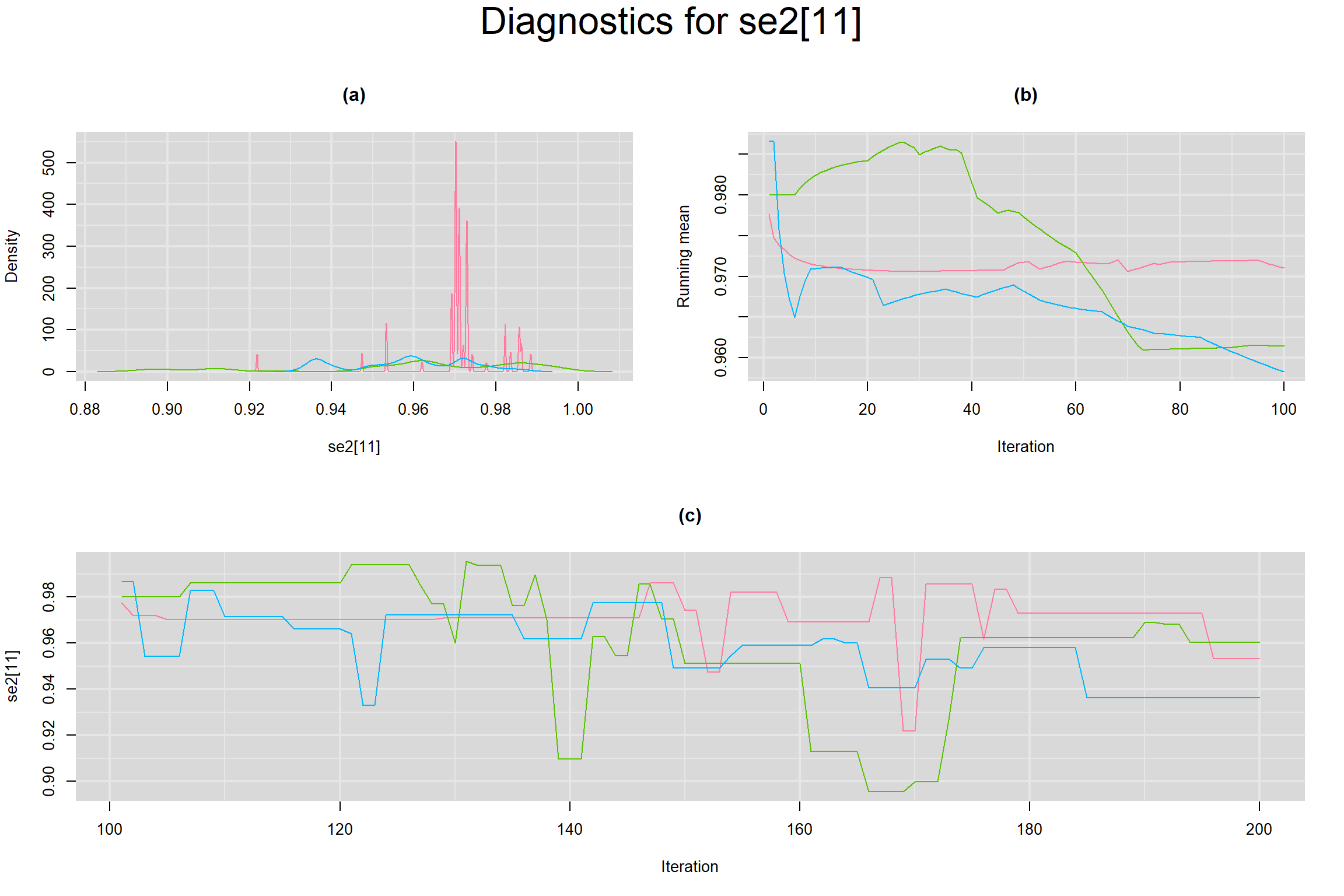
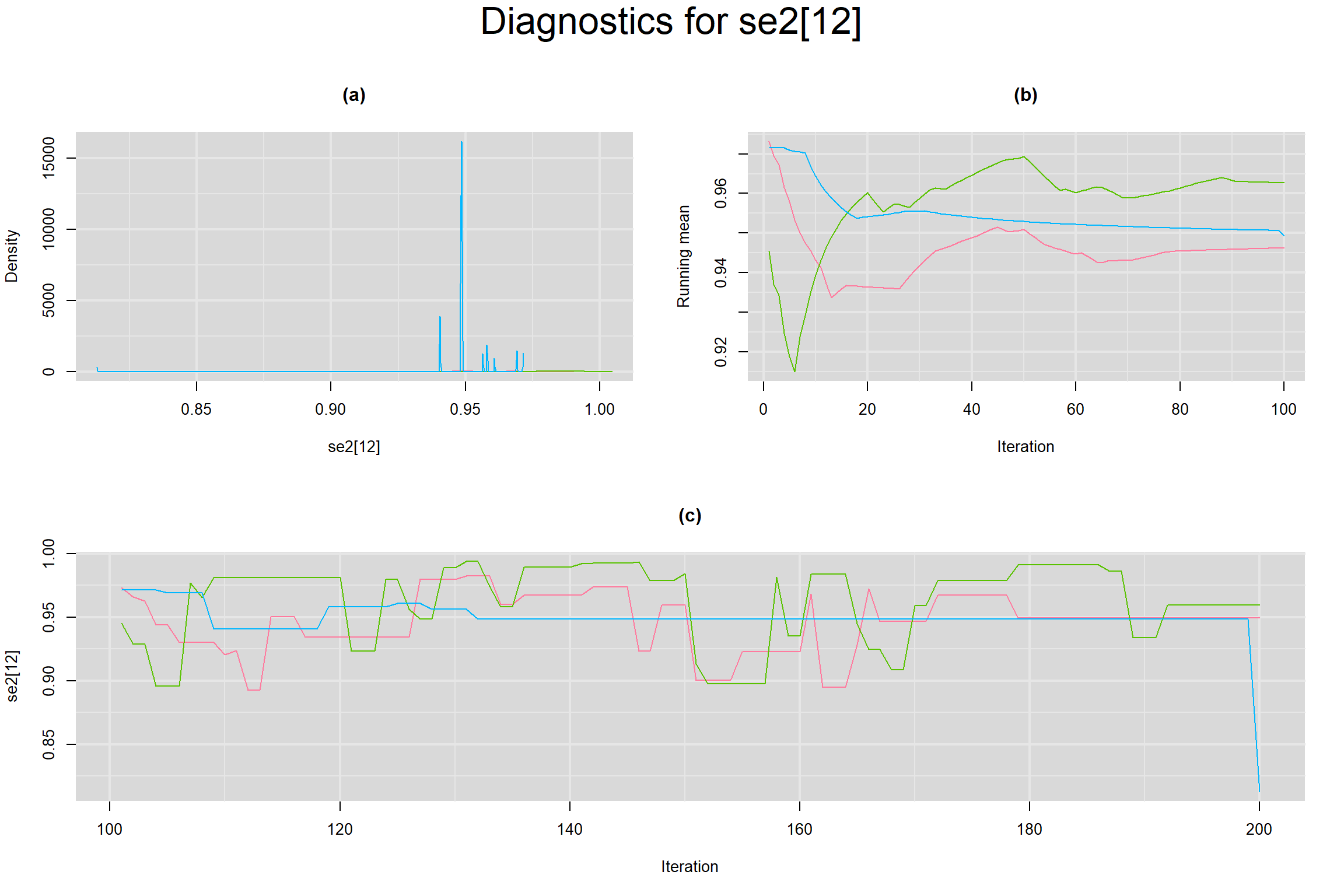
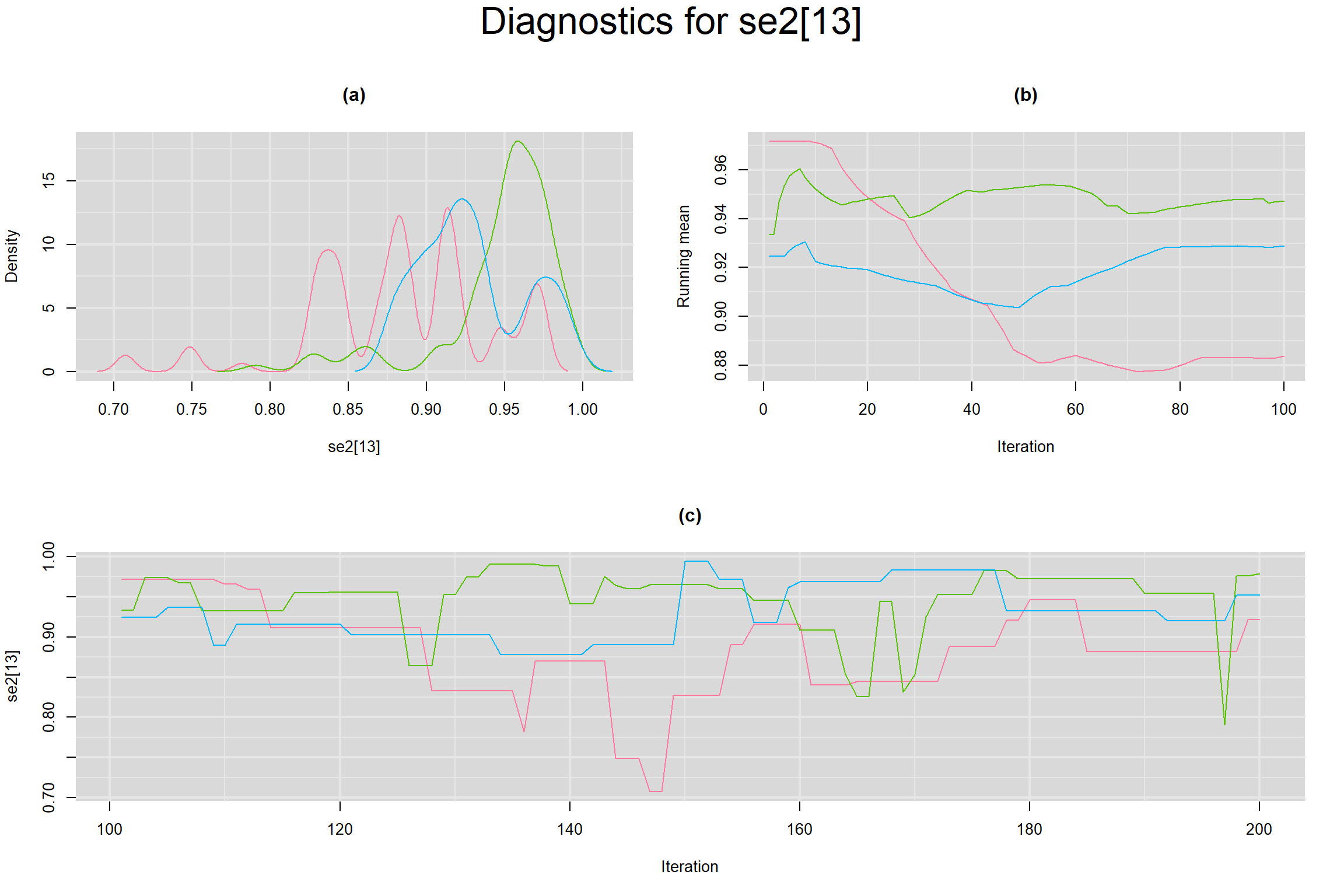
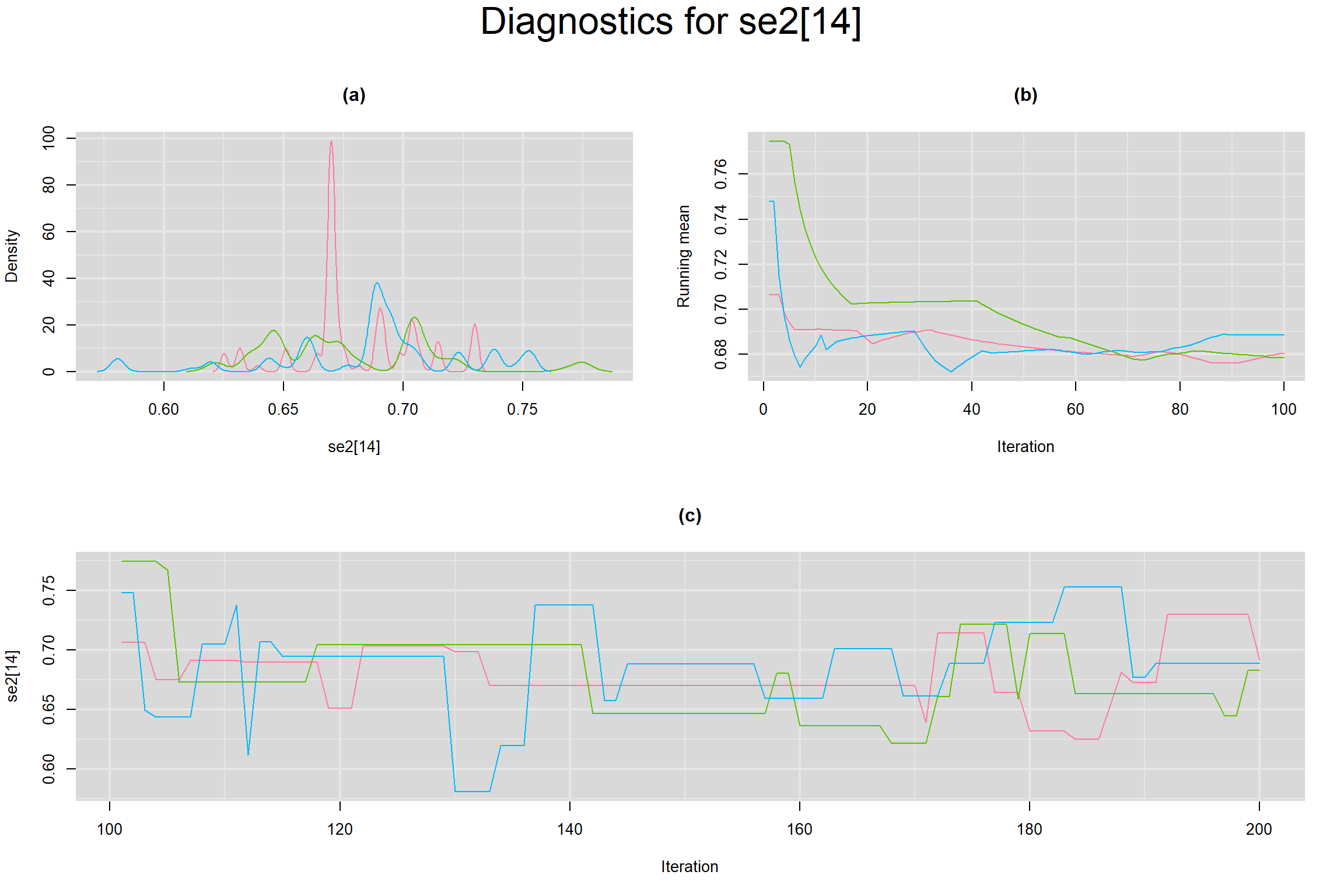
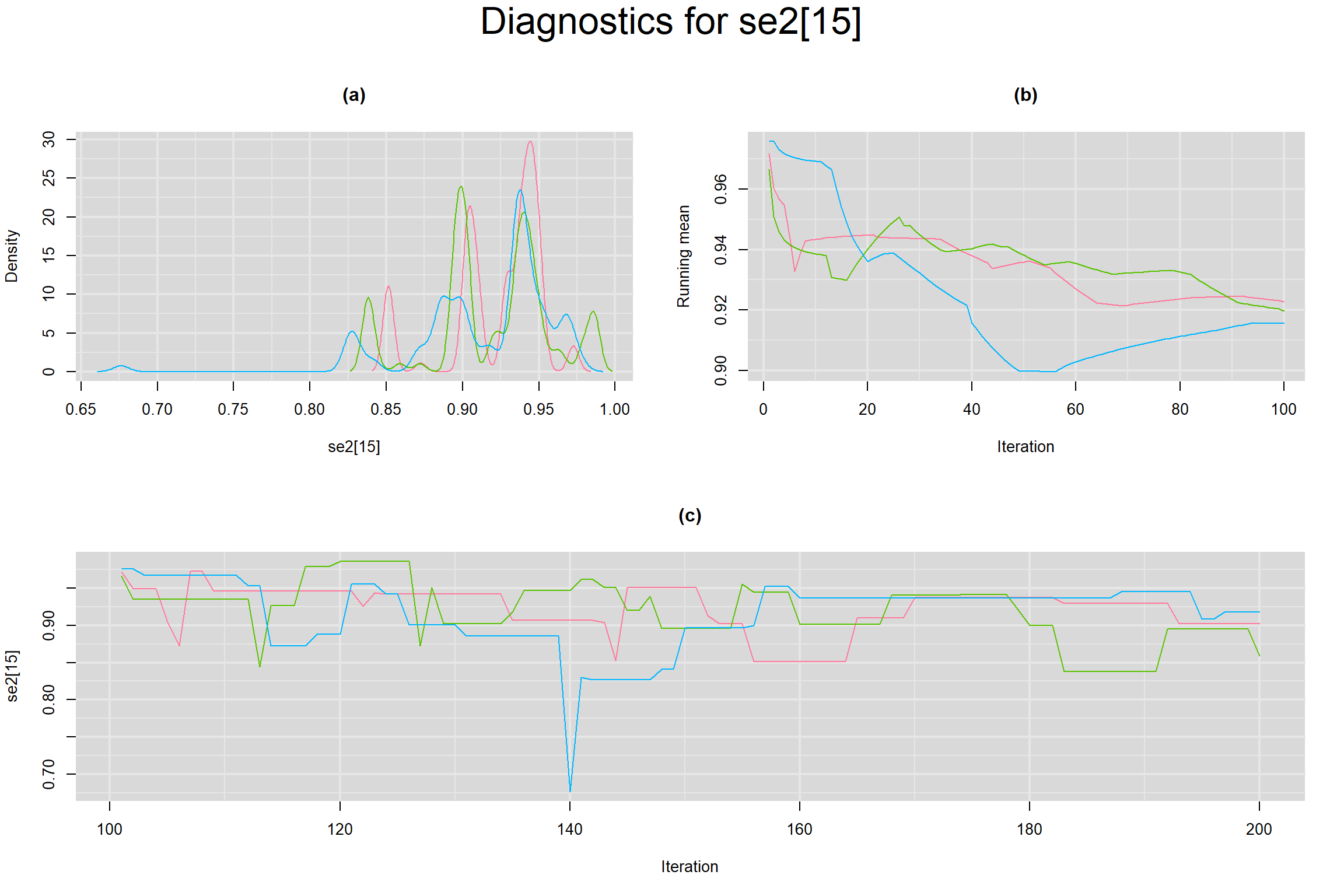
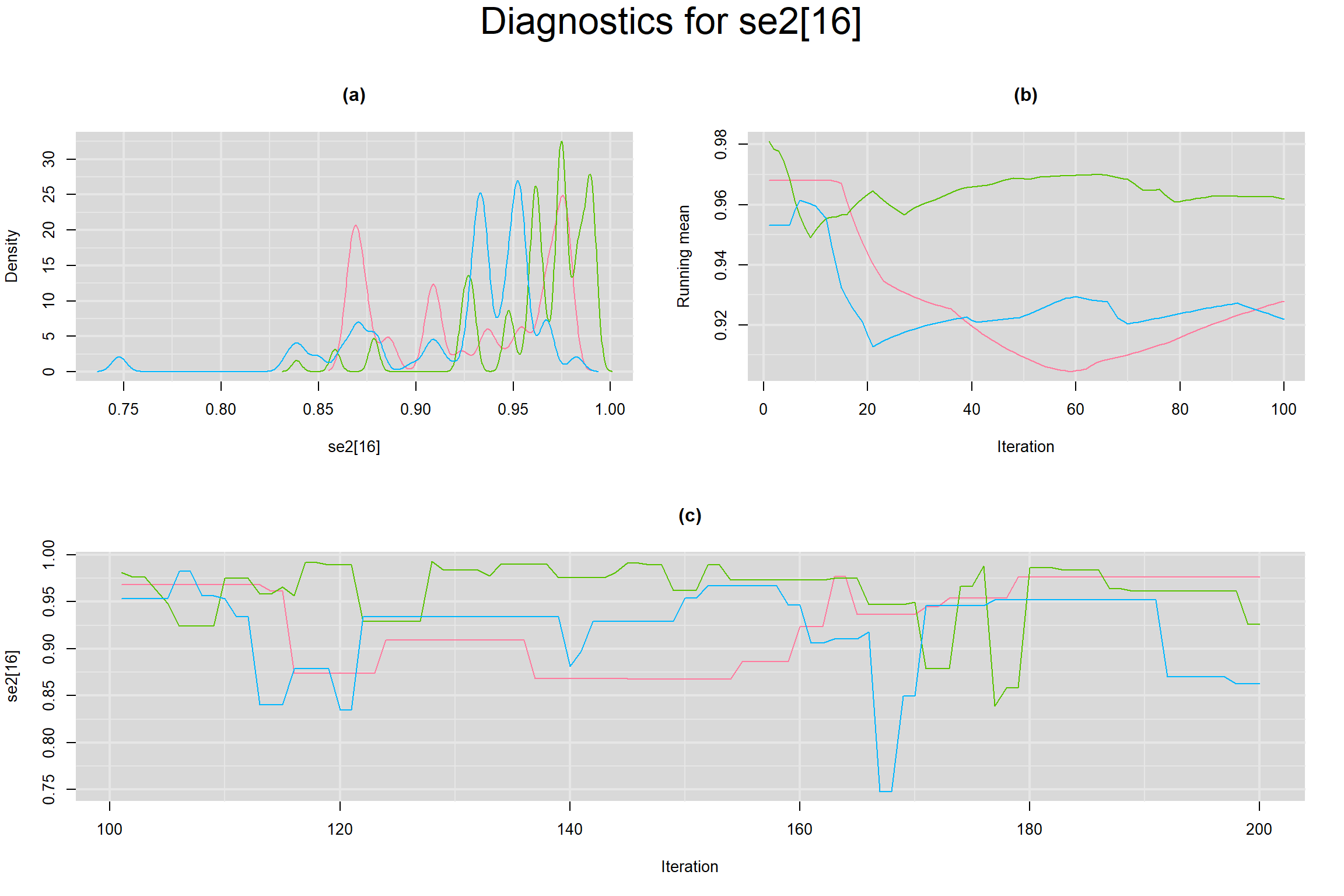
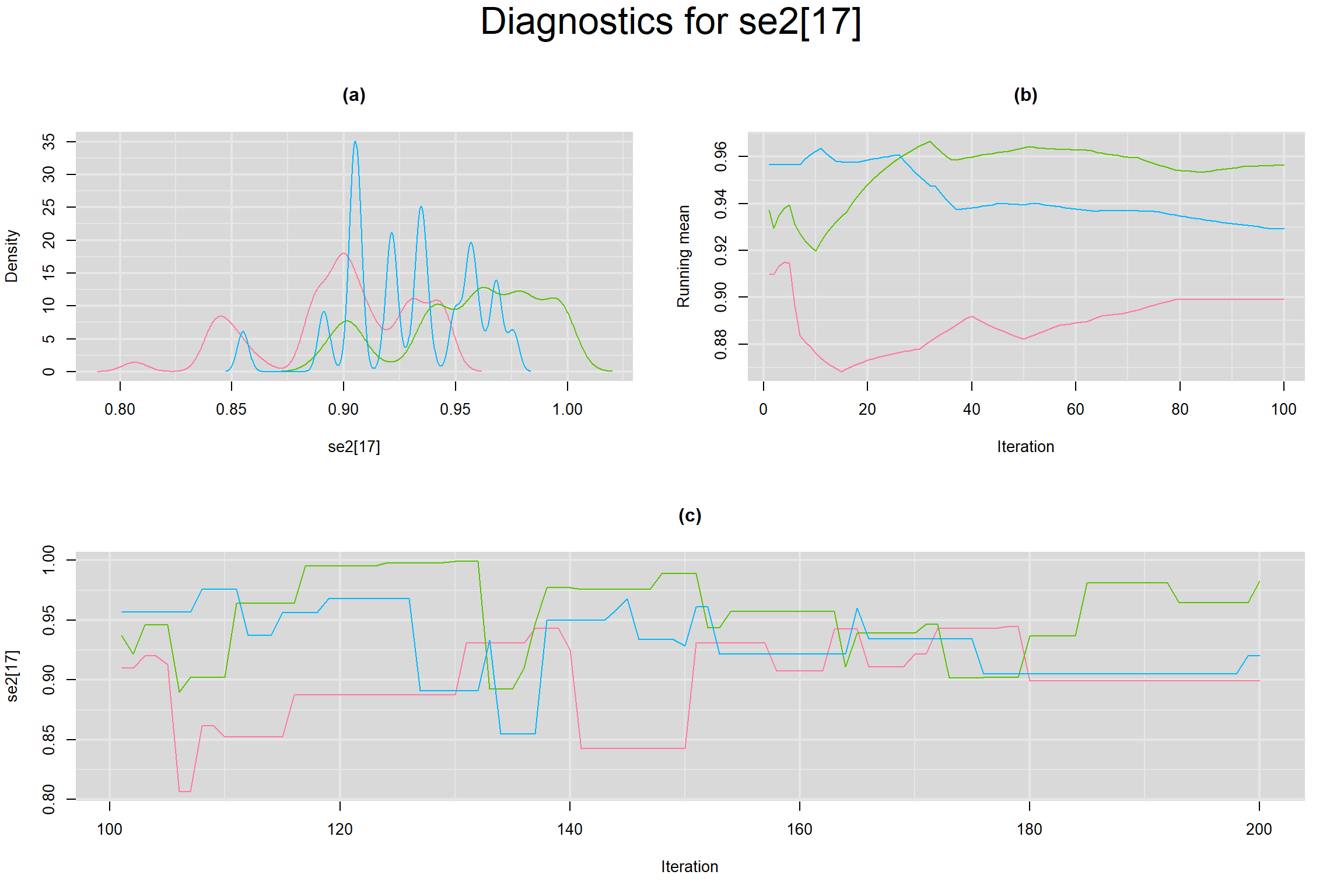
SPECIFICITY IN INDIVIDUAL STUDIES
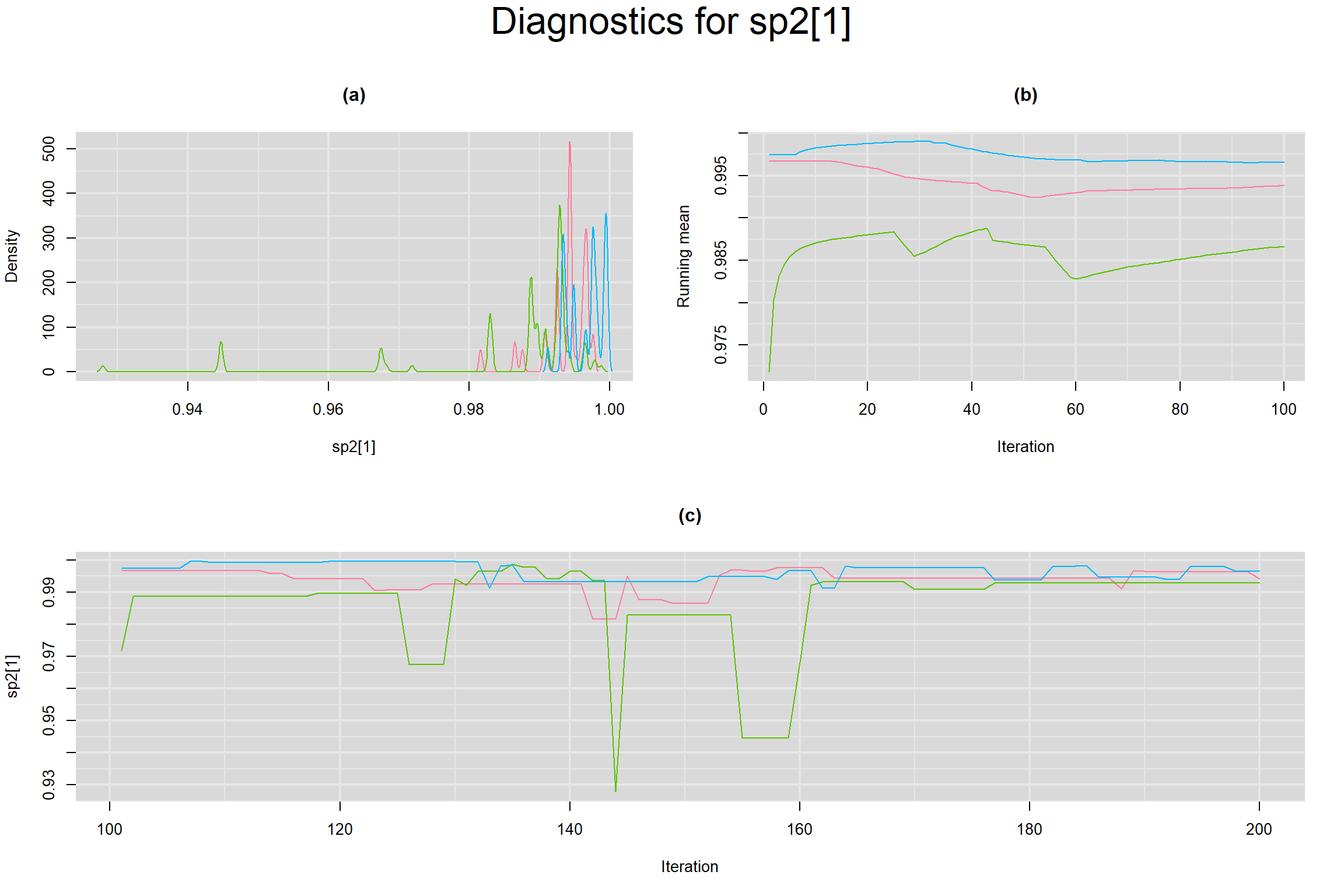
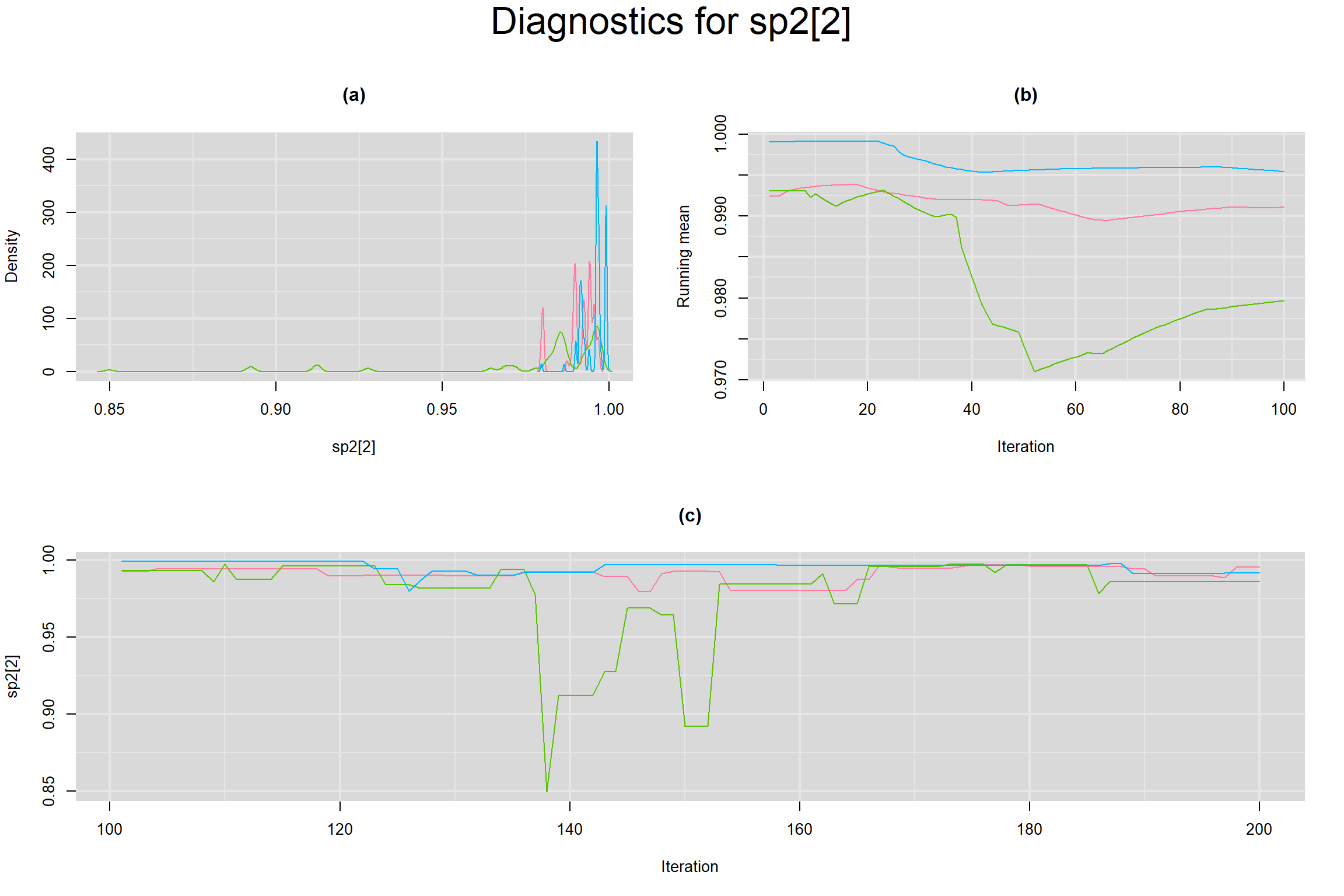
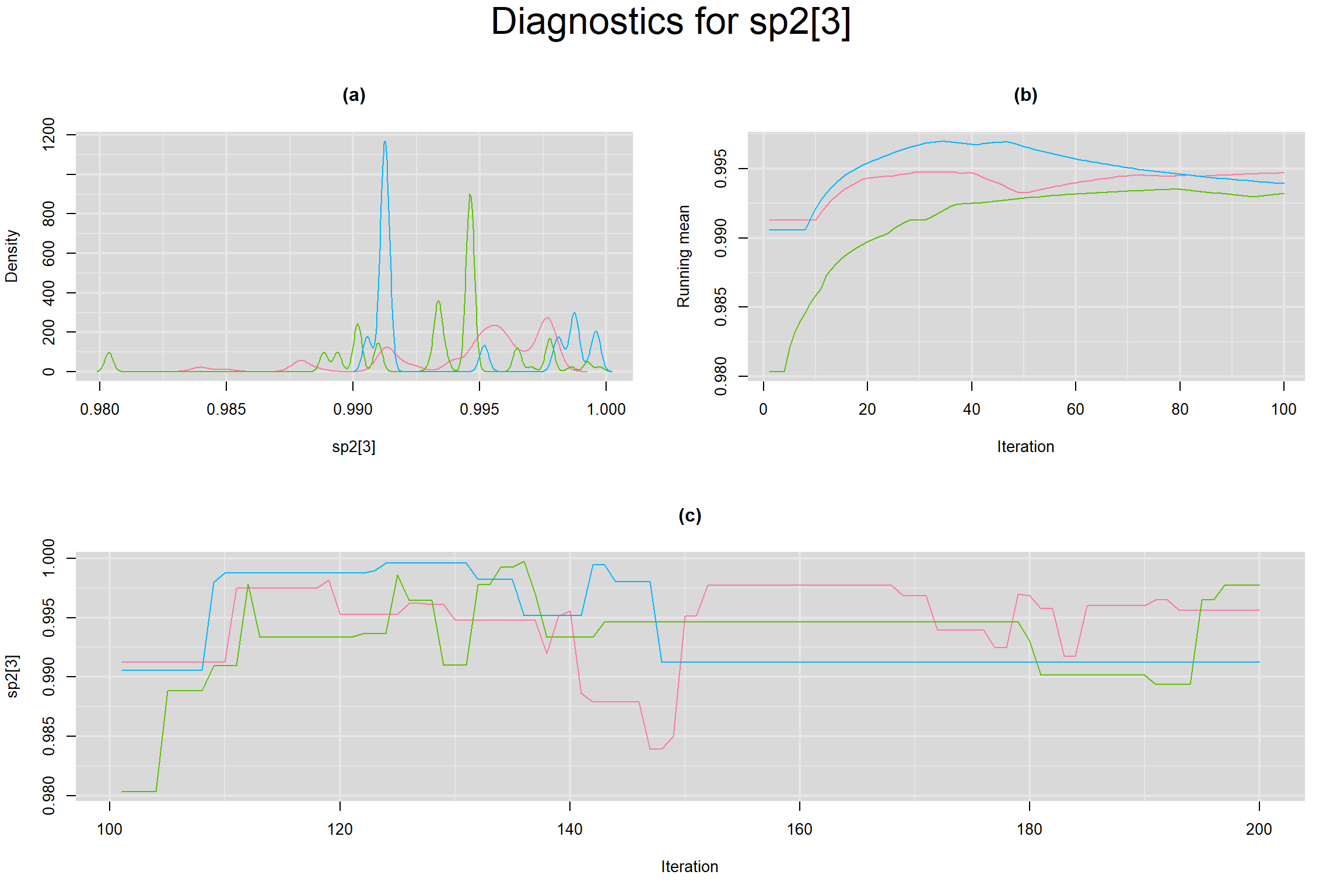
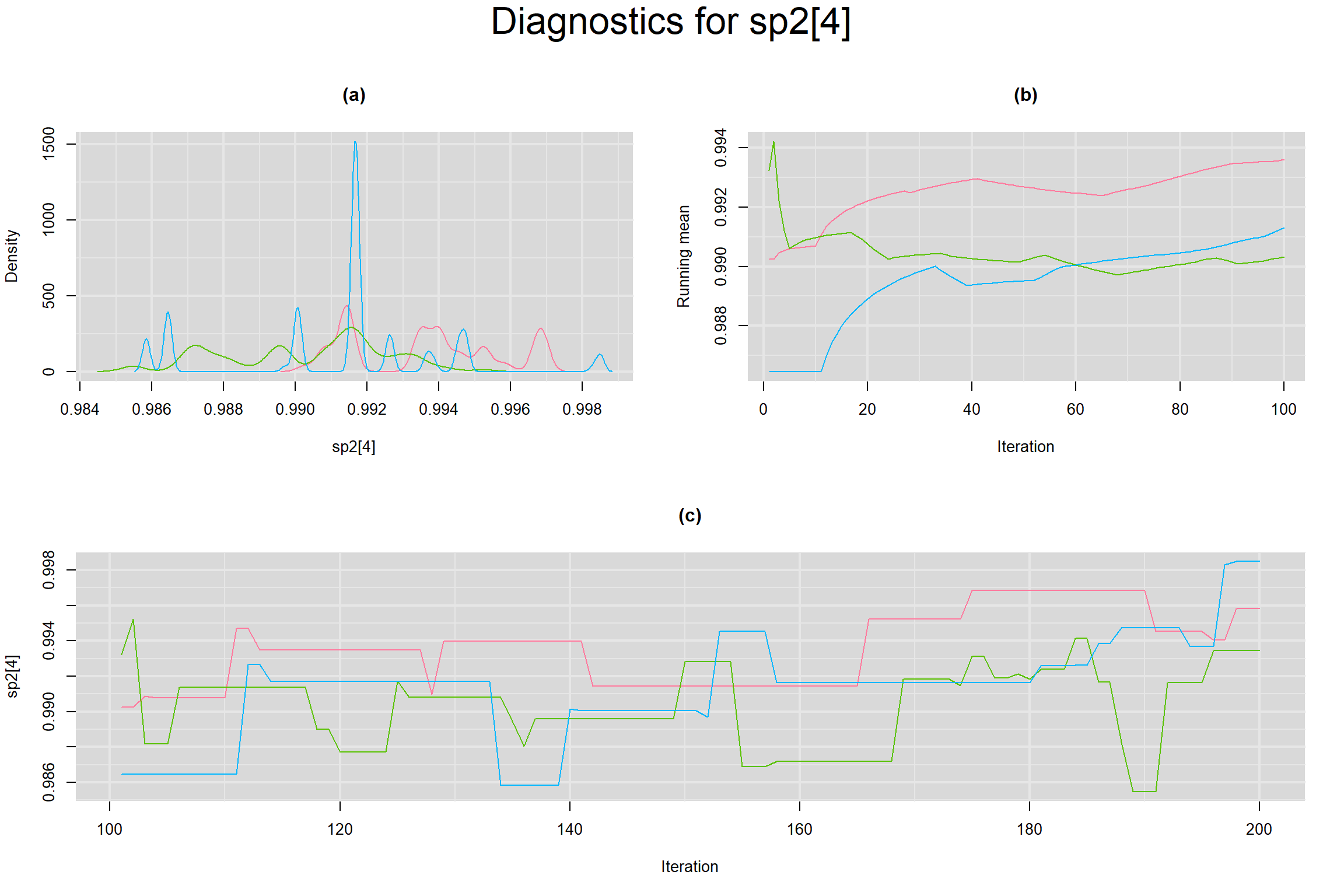
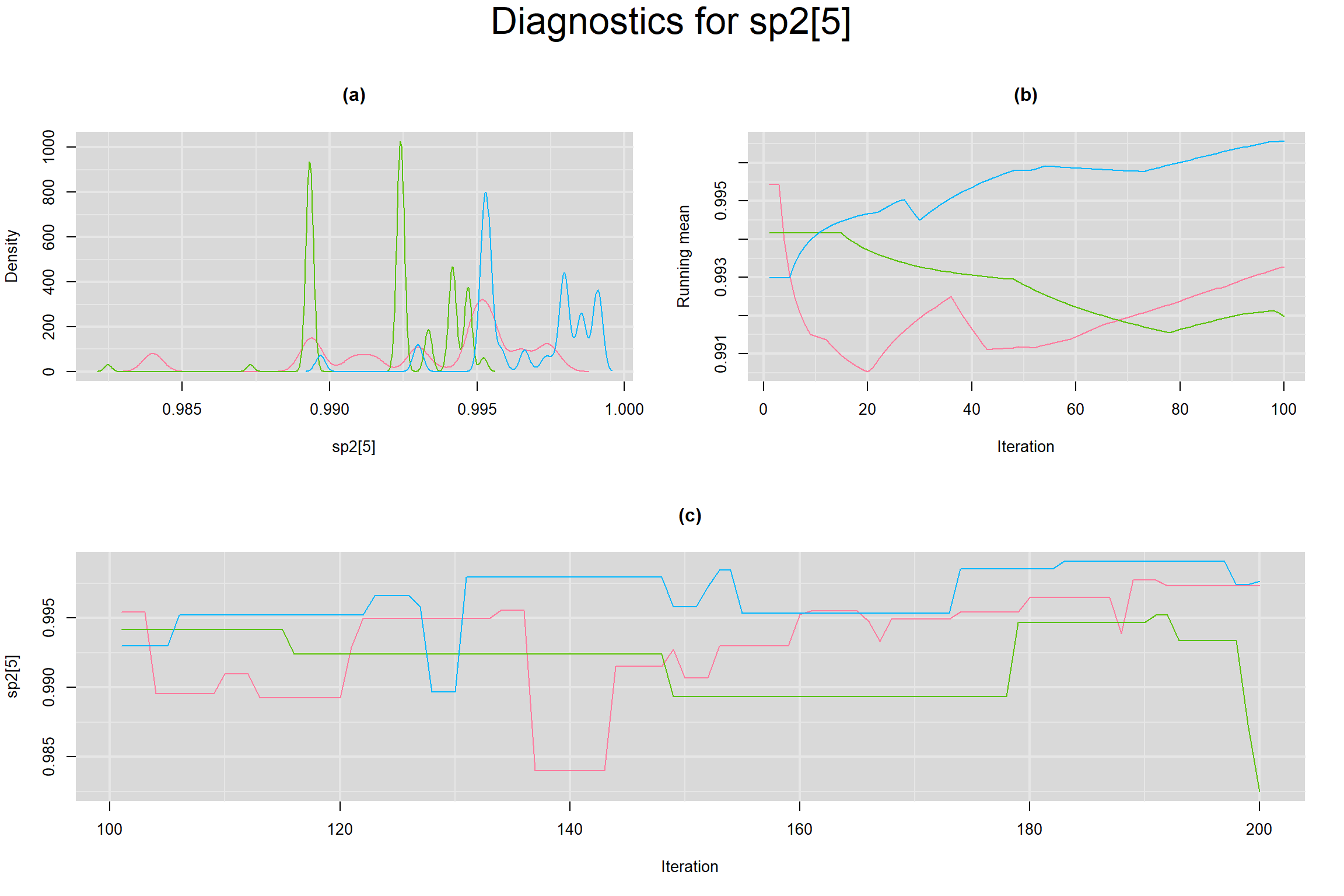
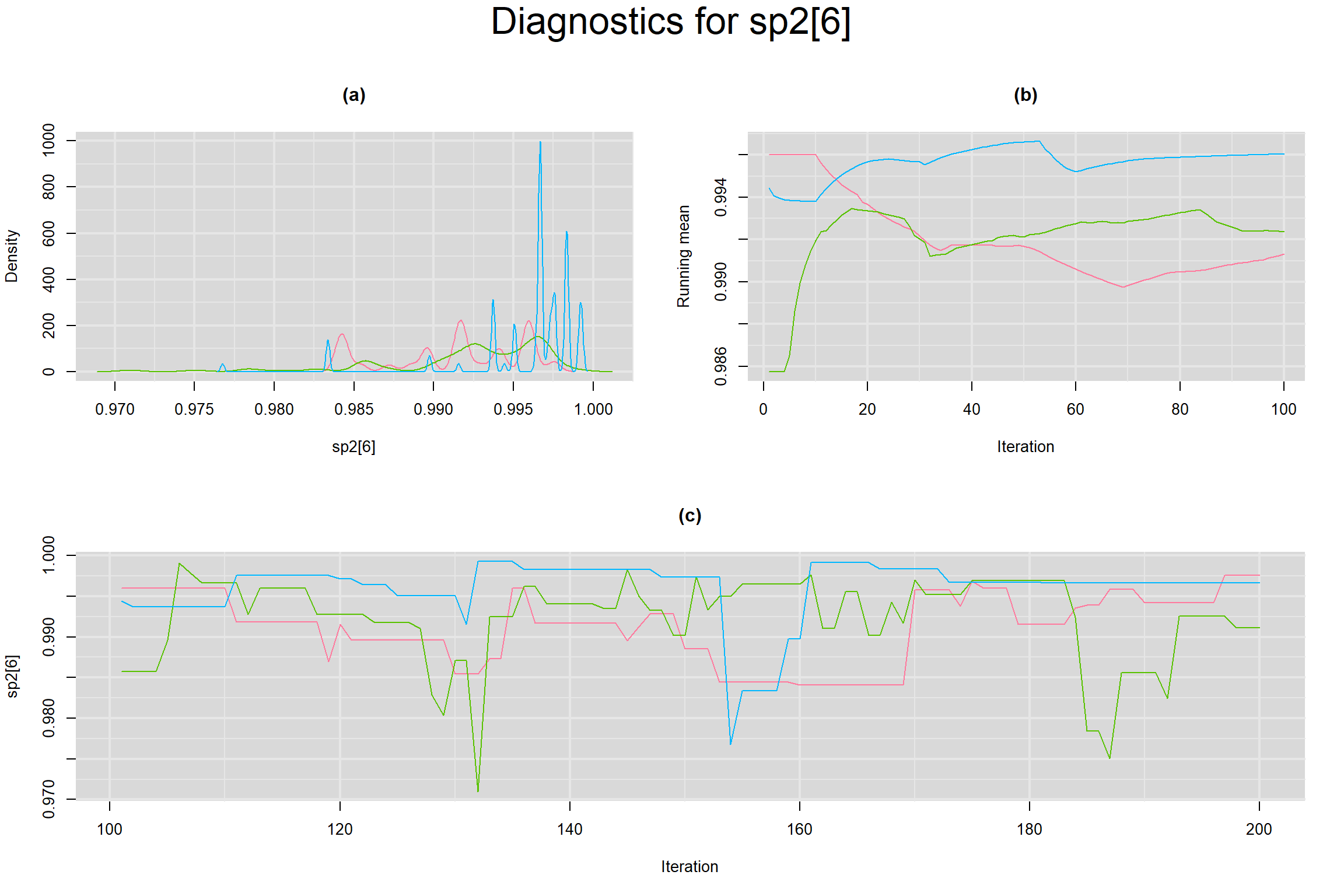
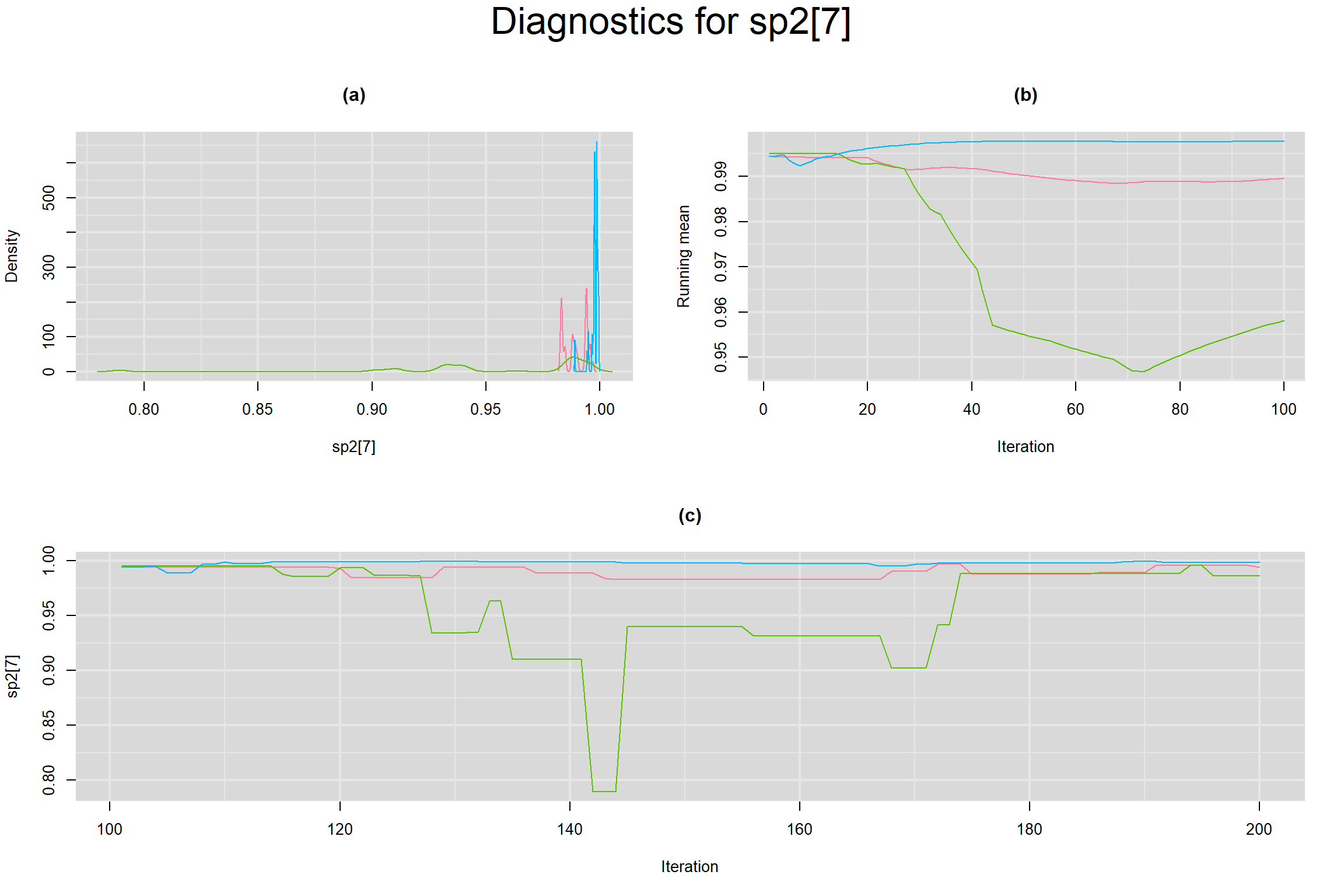
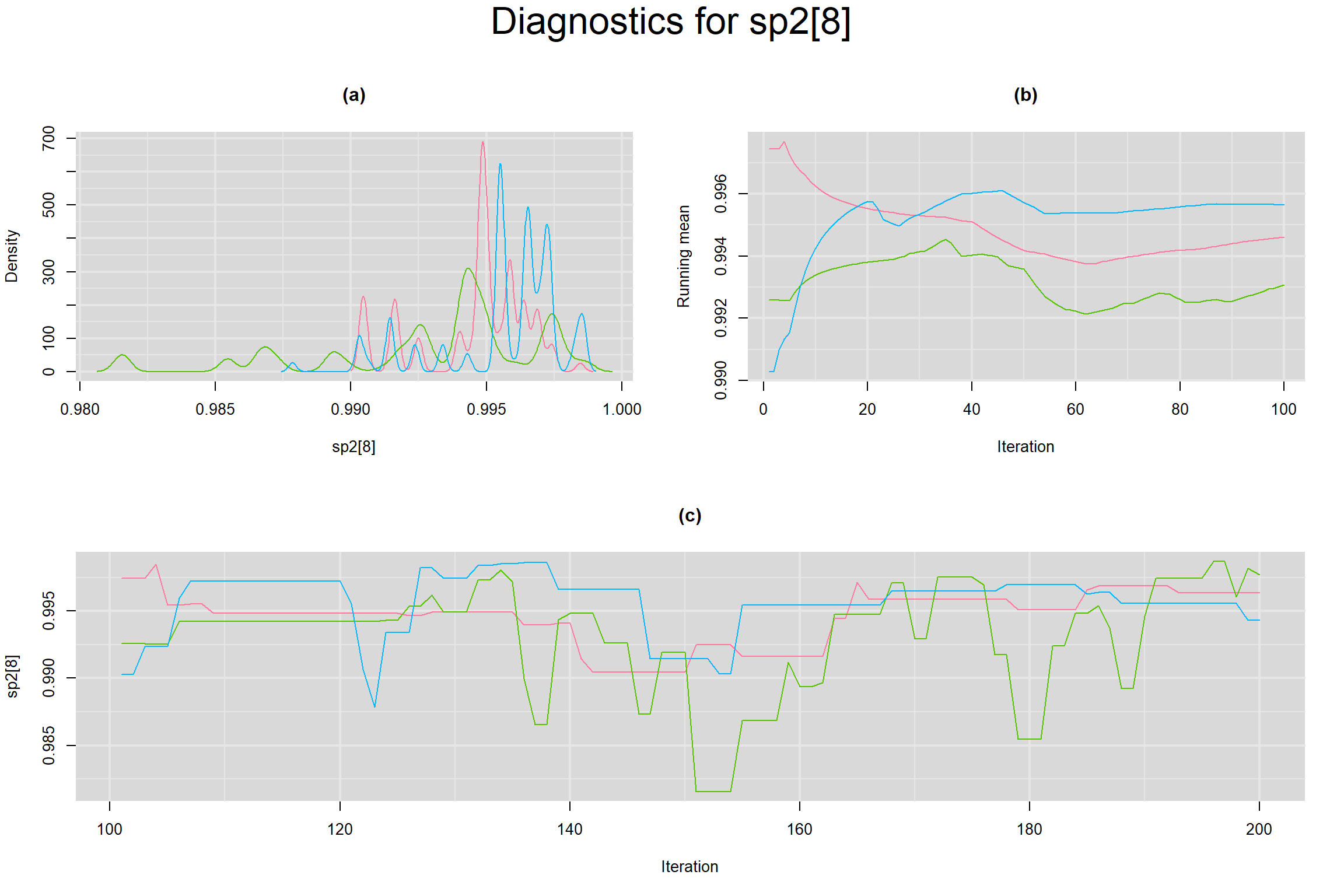
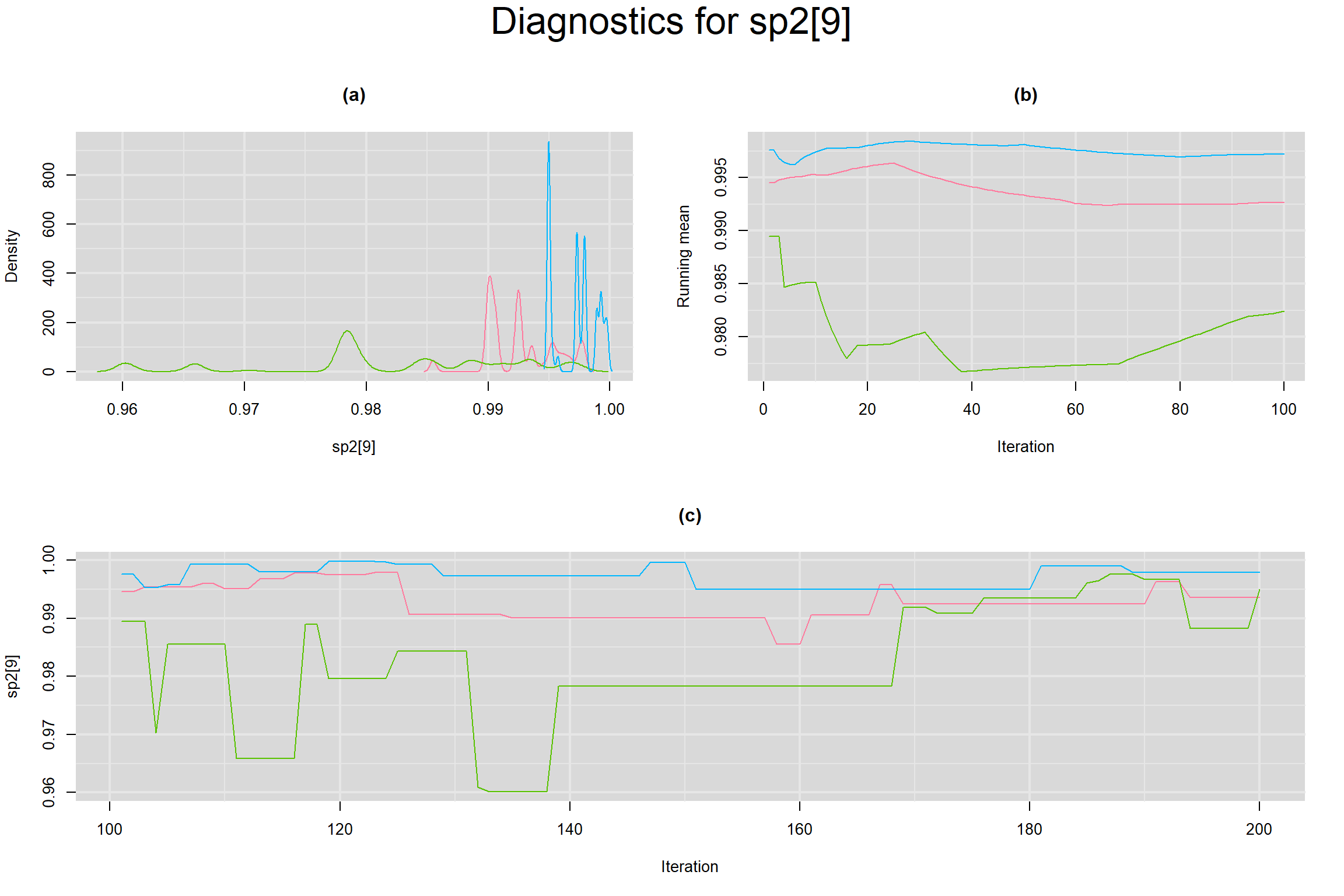
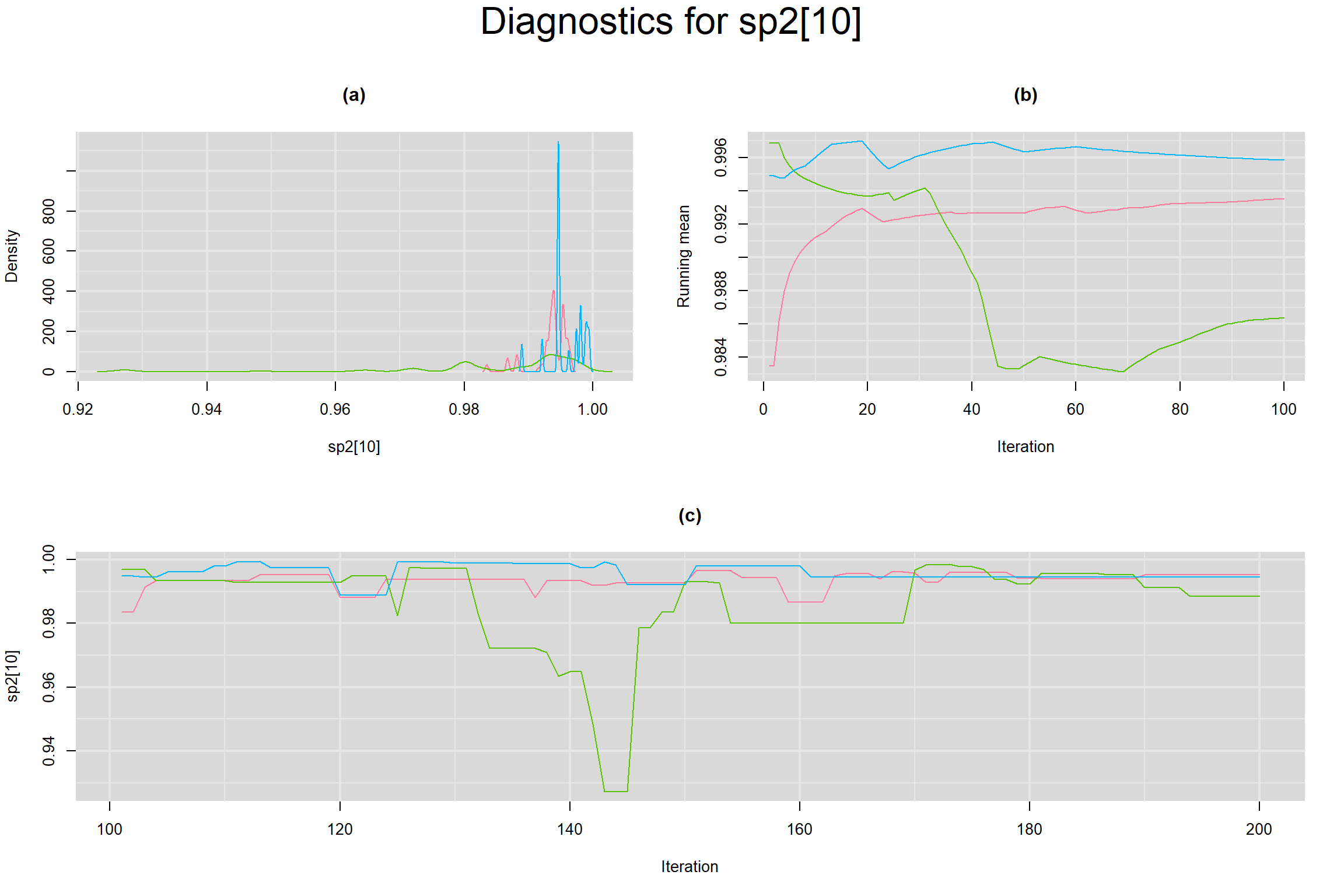
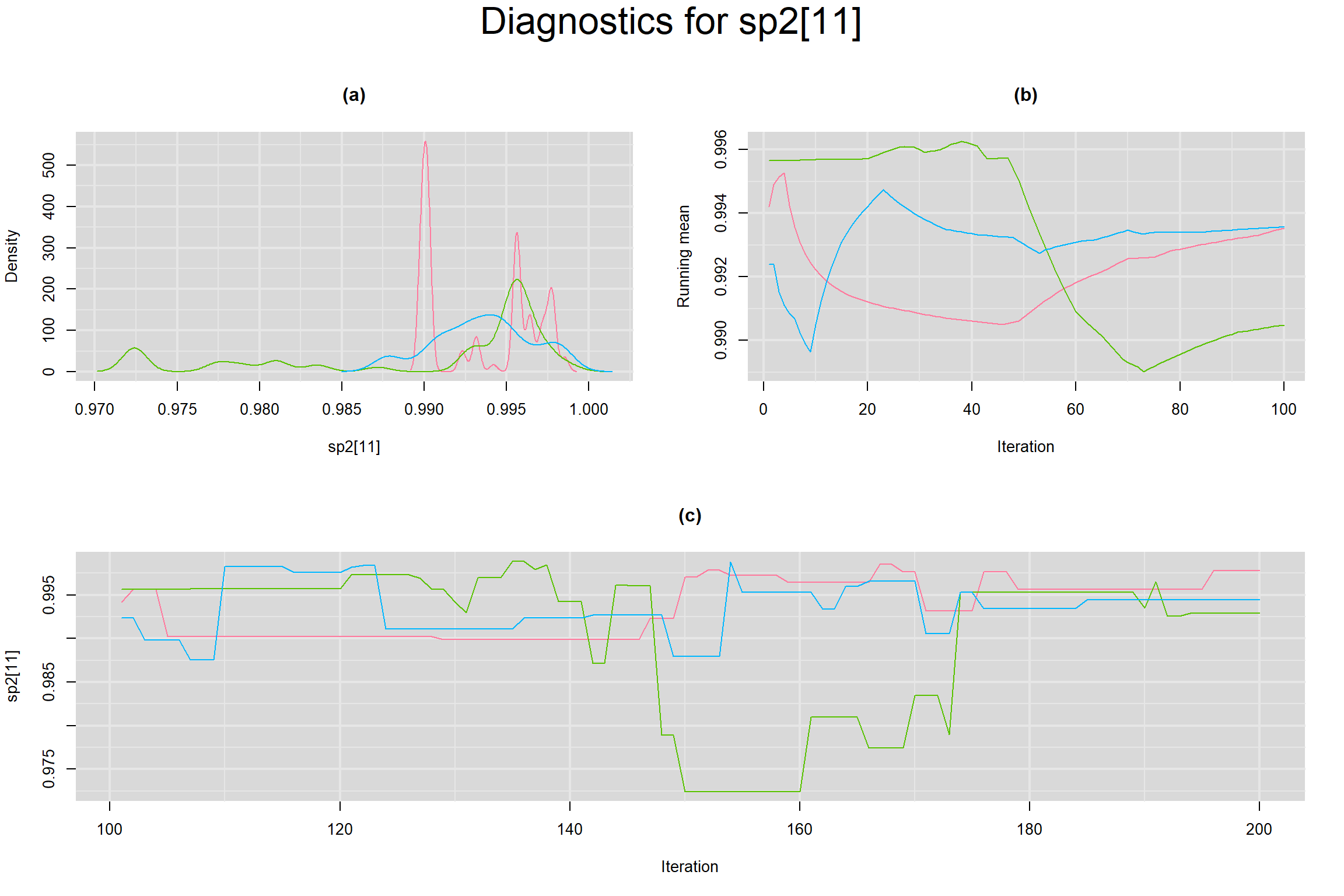
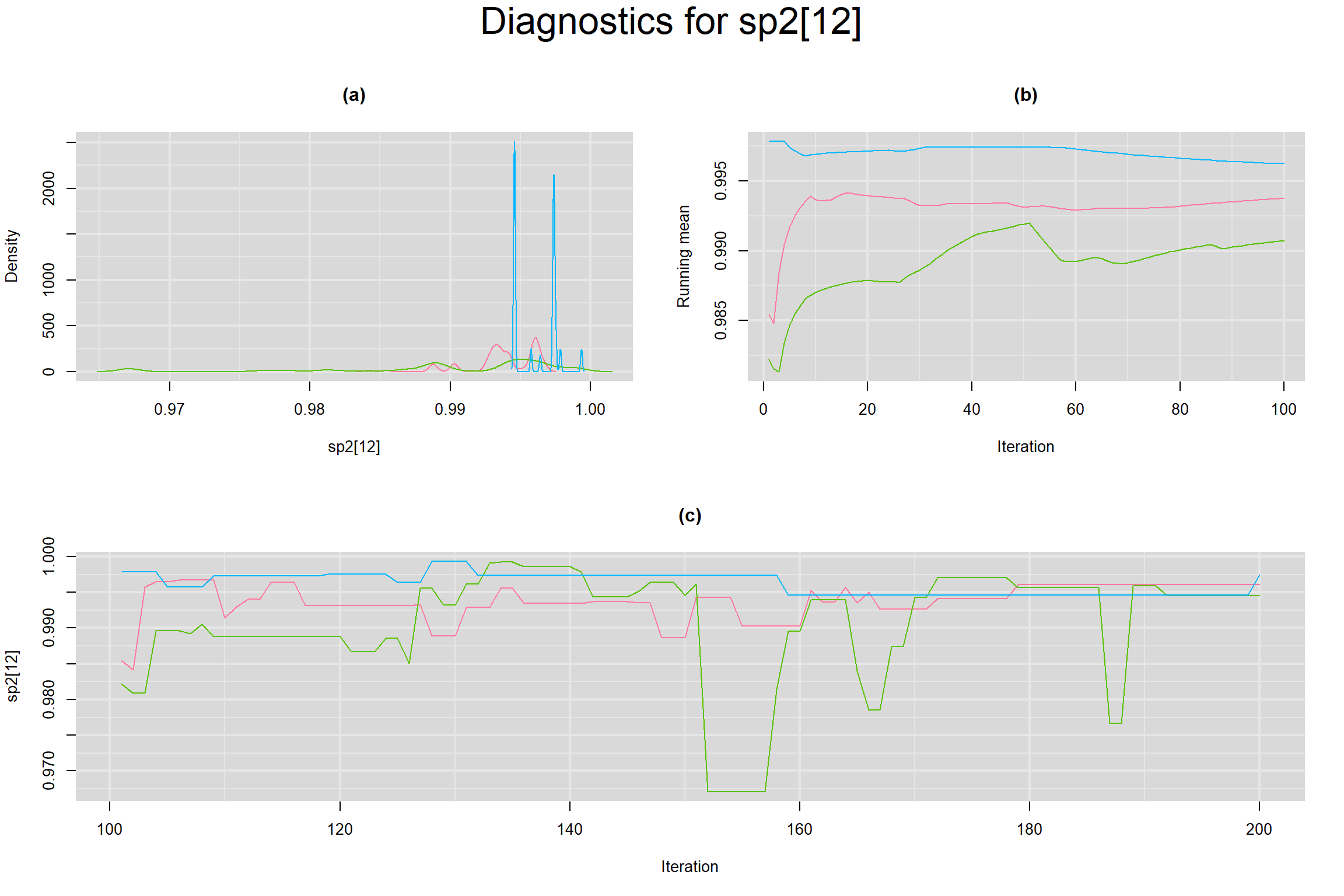
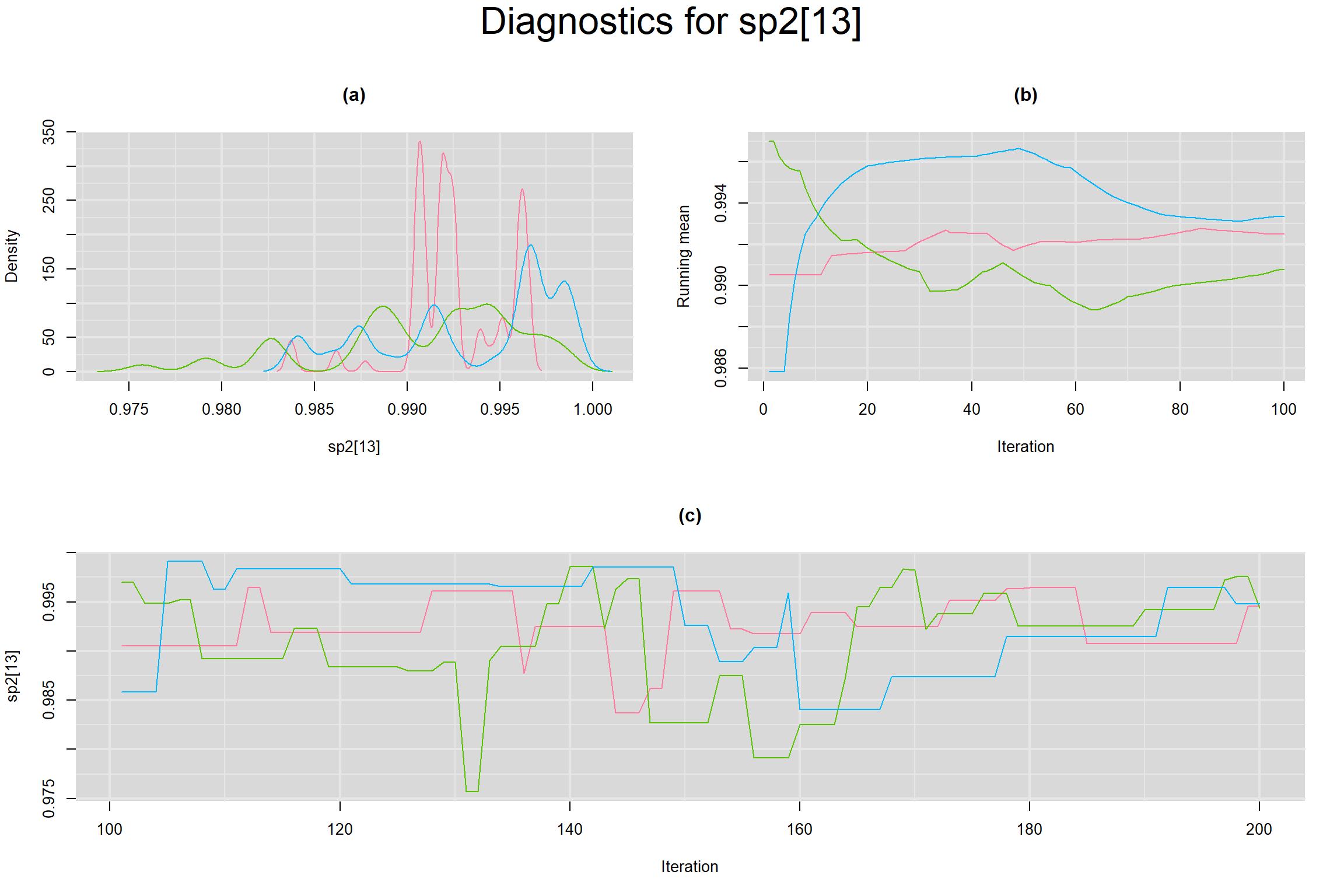
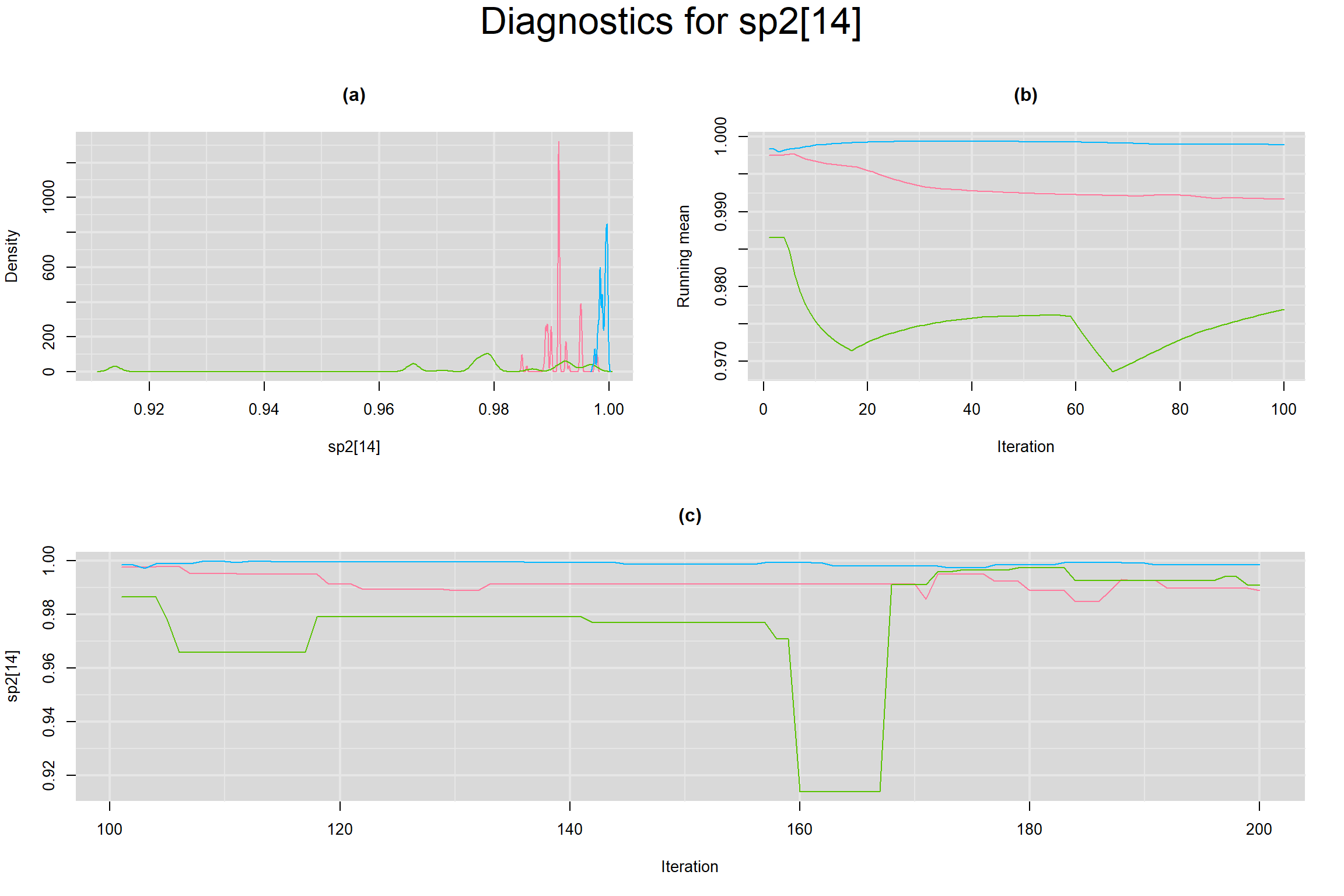
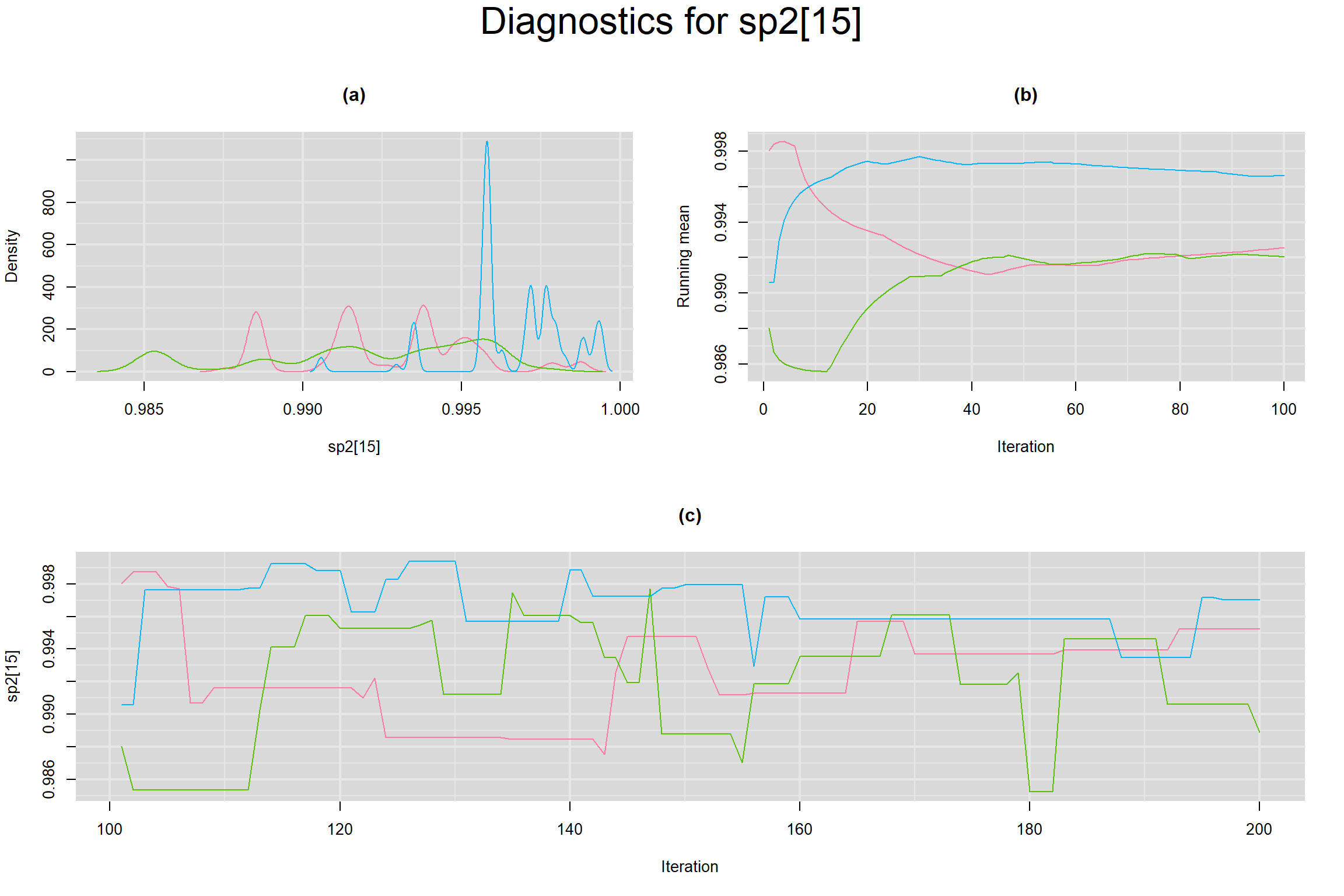
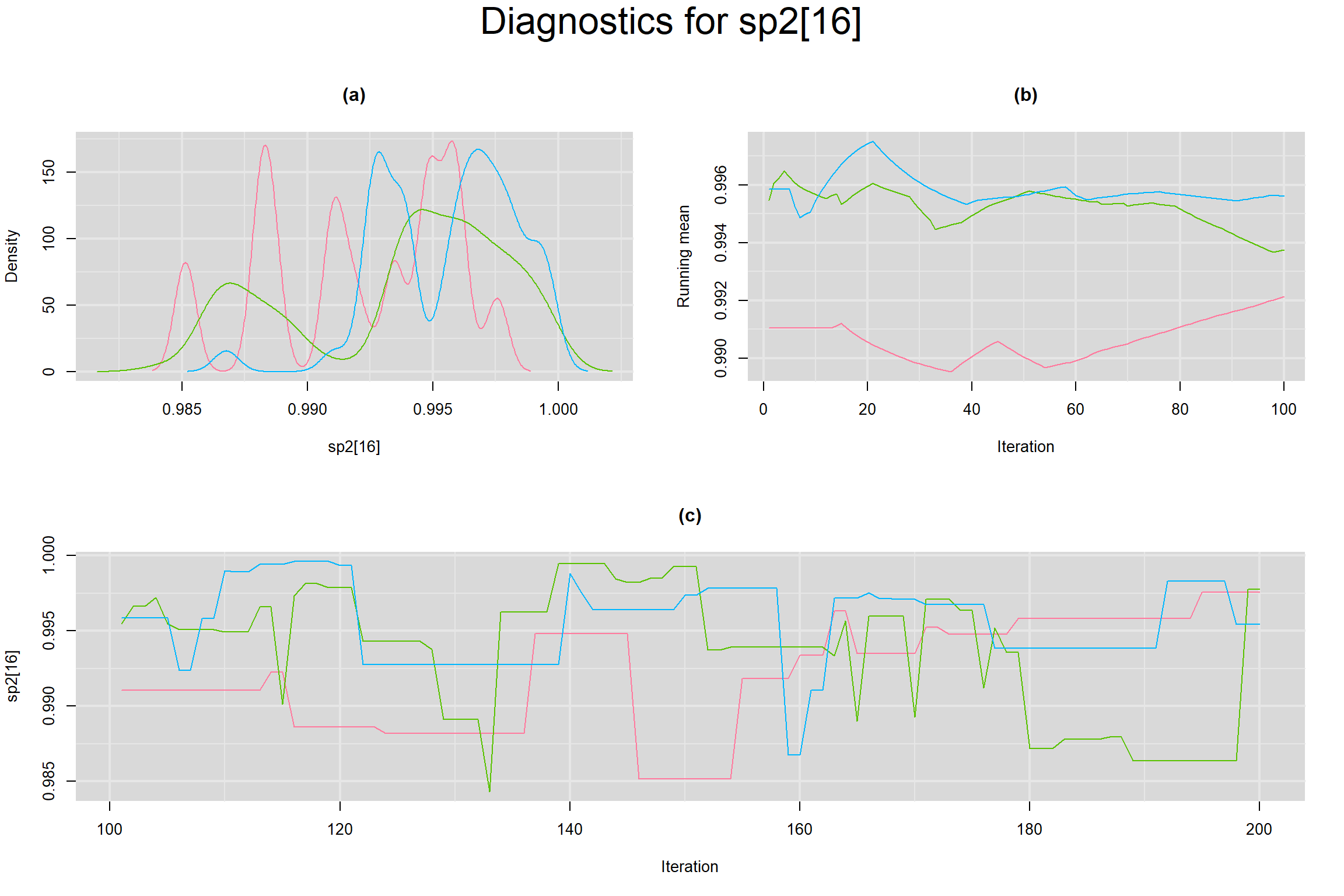
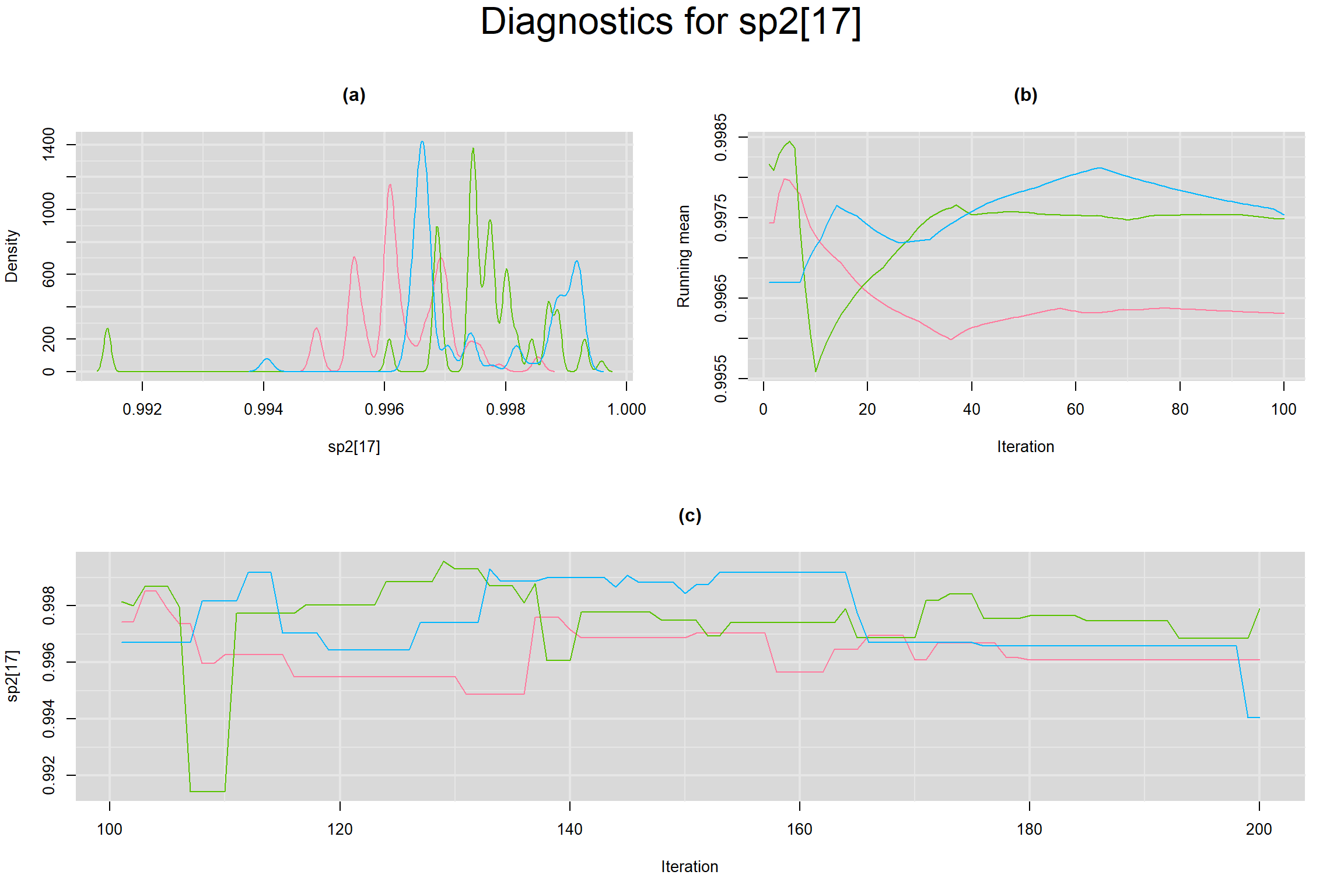
BETWEEN-STUDY VARIANCE IN THE LOGIT-TRANSFORMED SENSITIVITY AND SPECIFICITY
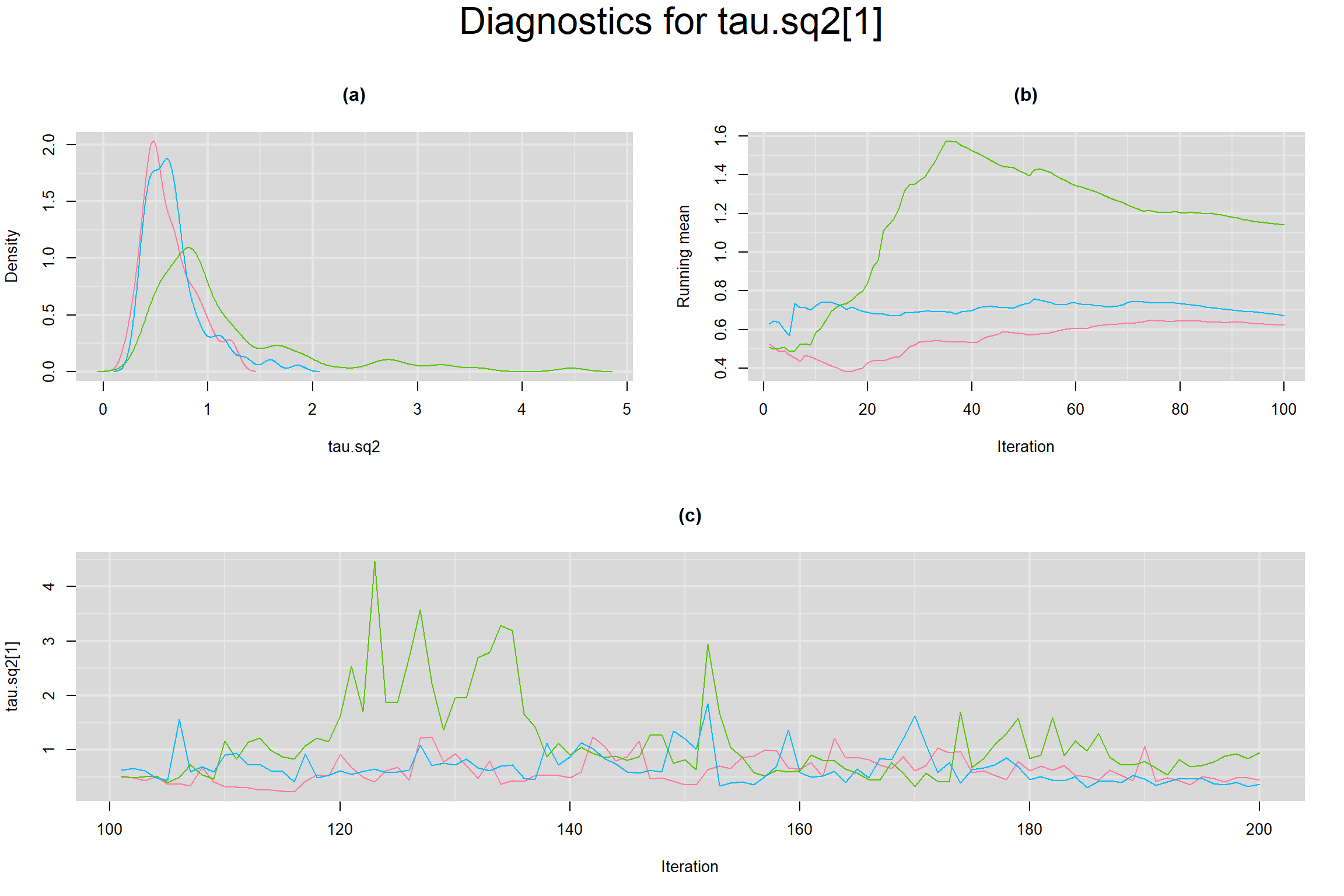
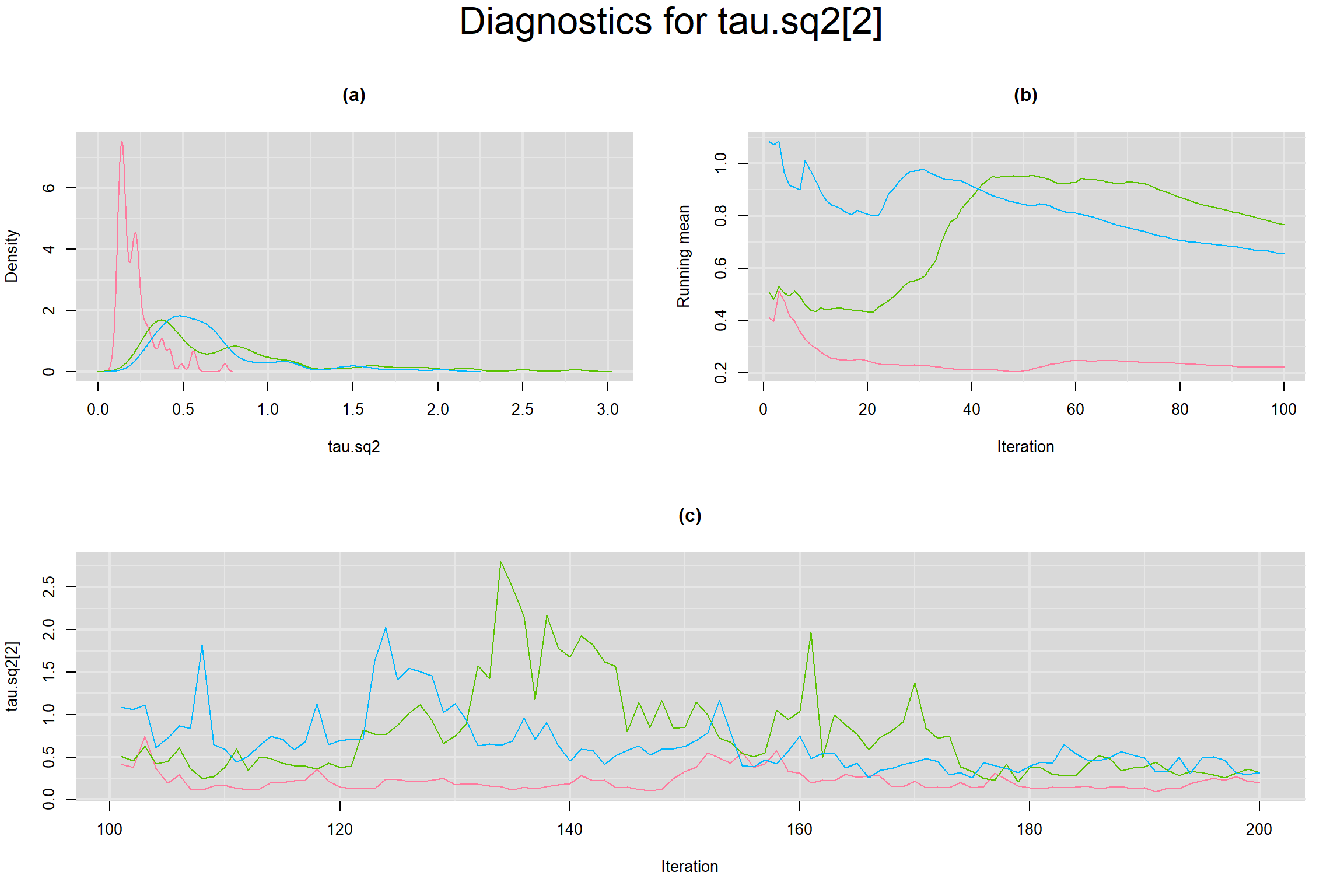
BETWEEN-STUDY STANDARD DEVIATION IN THE LOGIT-TRANSFORMED SENSITIVITY AND SPECIFICITY
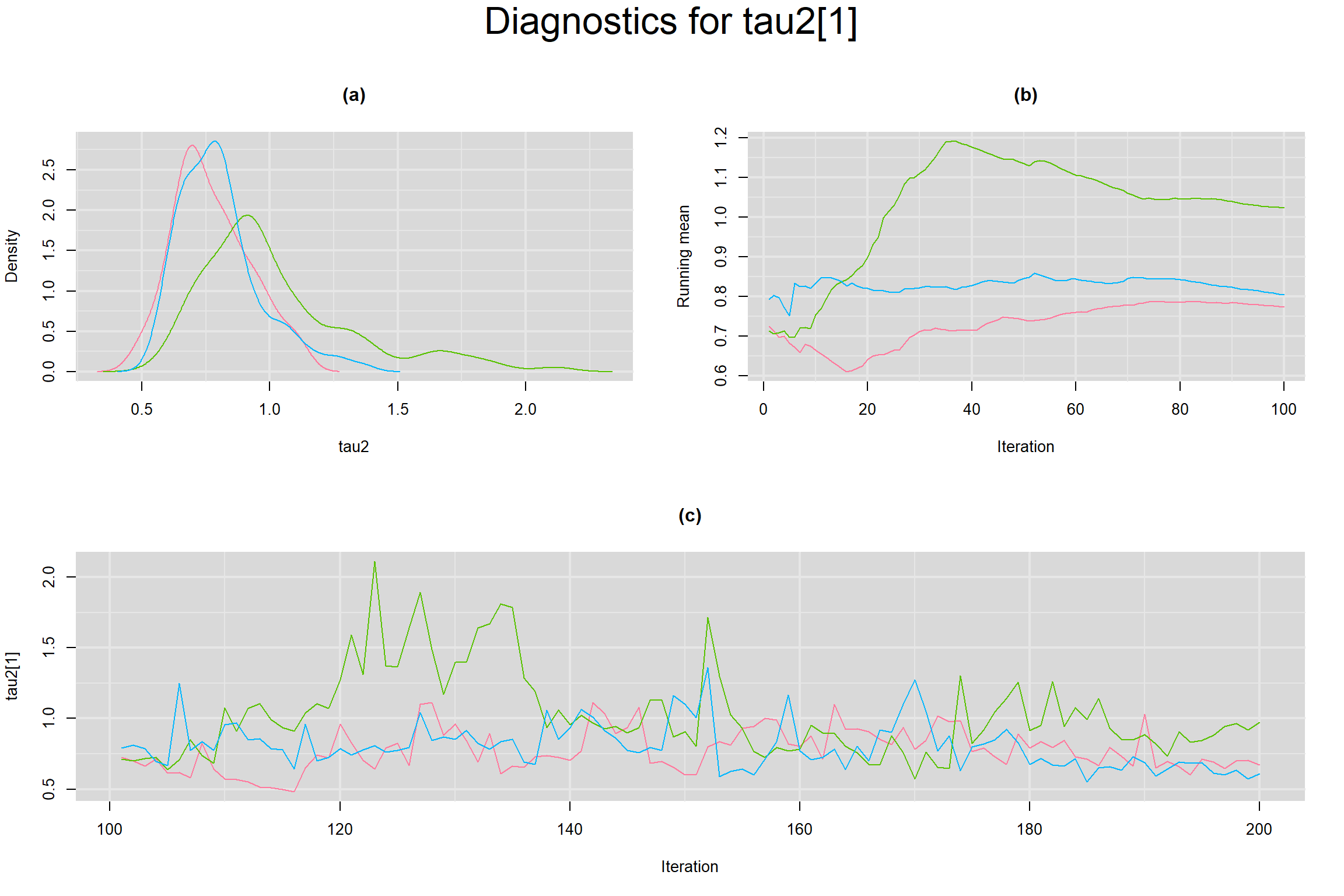
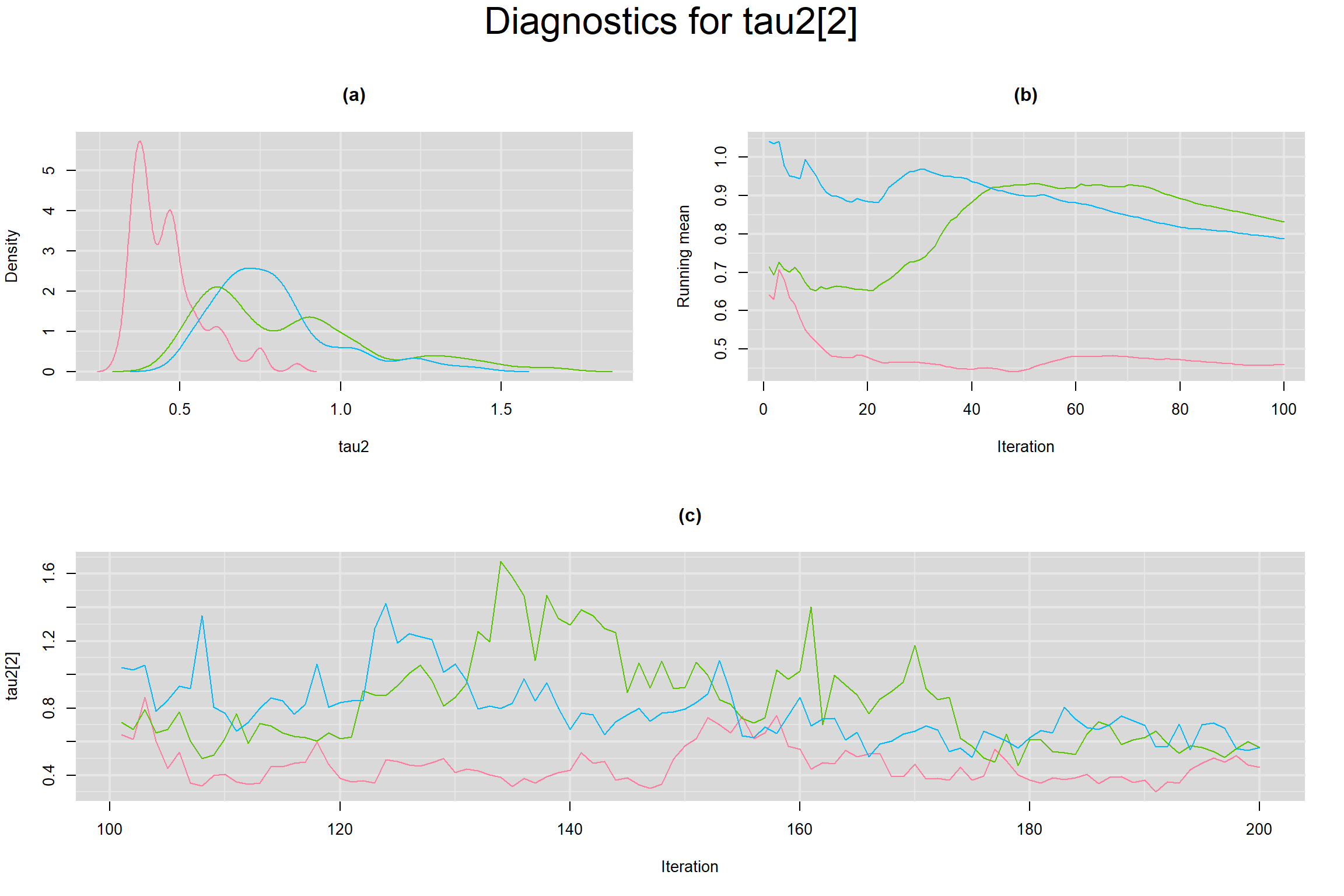
BETWEEN-STUDY PRECISION IN THE LOGIT-TRANSFORMED SENSITIVITY AND SPECIFICITY


PREVALENCE IN EACH STUDY

REFERENCES
Brooks, S. P., and Gelman, A. 1998. “General methods for monitoring convergence of iterative simulations.” Journal of Computational and Graphical Statistics, no. 7: 434–55.
Butler-Laporte, G, Lawandi, A, Schiller, I, Yao, M, Dendukuri, N, McDOnald, E. G. and Lee, T. C. 2021. “Comparison of Saliva and Nasopharyngeal Swab Nucleic Acid Amplification Testing for Detection of SARS-CoV-2; A Systematic Review and Meta-analysis.” JAMA Intern Med.
Gelman, A, Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A and Rbin, D. B. 2013. “Bayesian Data Analysis.” Chapman & Hall/CRC Press, London, Third Edition.
Gelman, A, and Rubin, D. B. 1992. “Inference from iterative simulation using multiple sequences.” Statistical Sciences, no. 7: 457–72.
Xie, X, A Sinclair, and N Dendukuri. 2017. “Evaluating the accuracy and economic value of a new test in the absence of a perfect reference test.” Res Synth Methods, no. 8(3): 321–32.